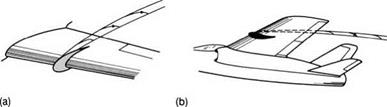
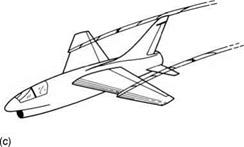
Flight with separated flow
On older aircraft types, it is normally necessary to avoid flow separation and stalling, since it is very difficult to maintain proper control in the stalled
|
|
|
Fig. 1.19 Flow separation At high angles of attack, as in the lower photograph, the flow no longer follows the contours of the upper surface, but ‘separates’, producing a highly turbulent recirculating region of flow (Photo courtesy of ENSAM, Paris) |
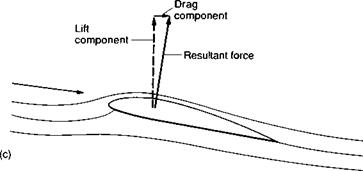
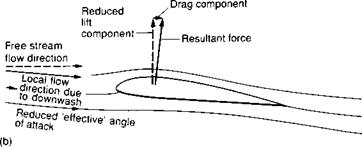
condition. However, from Fig. 1.17, you will see that after an initial drop at stall, the lift starts to rise again at high angles of attack. For thin wings, the highest value of CL may indeed be obtained in the stalled condition. The overall aircraft lift is further increased by the fact that at these high angles of attack, the engine thrust begins to add a significant component to the lift. Such high lift can be a considerable advantage to combat aircraft performing violent manoeuvres, since it can be used to produce a large (centripetal) force for rapid pull-out from a dive. Alternatively, by rolling the aircraft on its side, the lift can be used to produce the cornering (centripetal) force for a rapid turn.
On missiles, where there is no loading on the pilot to consider, it is normal to make full use of this extended capability; indeed, missiles may spend short periods actually flying backwards after a sharp turn. In rapid manoeuvres, and with large amounts of available thrust, the high drag produced is unimportant.
The main difficulty of flight in separated flow is one of stability and control. The lift, drag, and most importantly, the position of the centre of lift, all vary rapidly. To overcome this problem, the aircraft may need artificial stability in the form of a quick-acting automatic control system. The development of reliable microelectronic systems has meant that it is now possible to fly in what would have previously been considered to be a highly unstable and dangerous condition. Recent combat aircraft have demonstrated controlled flight at angles of attack of more than 70°.
For military aircraft particularly, flight with separated flow provides considerable rewards in terms of improvements in both performance and manoeuvrability. However, even though it may be possible to control the aircraft in the stalled condition, the instability of the separated flow may still cause structural problems due to excessive buffeting. One solution is to control or stabilise the separated flow as described below.