From the results presented in Sections 4.4.2.1-4.4.2.3 for the three different cases Kang et al. [351] made the following observations: (i) the time-averaged force increases with increasing motion frequency; (ii) changes in structural properties, such as the thickness ratio, Young’s modulus, or wing density (mass), lead to a non-monotonic response in the force generation; and (iii) for the hovering isotropic Zimmerman wing, the ratio between the density ratio and the effective stiffness is monotonic with the time-averaged lift generation. To explain the observed trends Kang et al. [351] mainly analyzed the physics based on Eq. (4-1) with simplifying approximations for the fluid dynamic force, f*xt (see also Section 3.6.4), based on scaling arguments. The flow field and the structural displacement field should simultaneously satisfy Eq. (3-18) and Eq. (4-1); of these two equations Eq. (4-1) was considered, which has the advantage that it is linear, except for the fluid dynamic force term; in contrast, the Navier-Stokes equation is non-linear in the convection term. Subsequently, a relation between the time-averaged force and the maximum relative tip displacement was established by considering the energy balance.
To capture the essence of the mechanism involved in the force enhancement due to flexibility, it is necessary to analyze the interplay among the imposed kinematics, the structural response of the wing, and the fluid force acting on the wing. The derivation leading to the relation between the time-averaged force acting perpendicular to the wing motion, (Cp) and the maximum relative tip deformation vmax is lengthy, where v* (x*, t*) = w* (x*, t*) – h(t*) is the displacement of the wing relative to the imposed kinematics motion; see Kang et al. [351] for the detailed steps. A treatment using simplifying approximations is helpful in enabling the analysis, but mainly serves to elucidate the scaling analysis and is not meant to offer a complete solution. Consider Eq. (4-26) in one dimension in space with 0 < x* < 1 and time
t* > 0, for the vertical displacement w*, with the wing approximated as a linear beam. A plunge motion, Eq. (3-12), is imposed at the leading edge at x* = 0. The trailing edge x* = 1 is considered as a free end (i. e., with the boundary conditions,
 |
w* (0, t *) = h(t *) = St cos(2n t *), к
and the initial conditions
*, * п дw*(x*, 0)
w* (x, 0) = St, = 0,
( ’ ) к, дt *
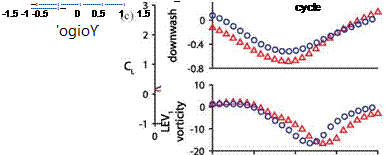
where the factors involving l/cm become unity for the chordwise flexible airfoil case). For the spanwise flexible wing and the isotropic Zimmerman wing cases that are discussed in Section 4.4.2.2 and Section 4.4.2.3, respectively, П0 and П need to be corrected as l/cm = AR. Following the procedure described in Mindlin and Goodman [511], a partial differential equation with homogeneous boundary conditions can be found by superimposing the plunge motion on the displacement v(x*, t*) = w(x*, t*) – h(t*). The consequence of having a sinusoidal displacement at the root is that the vibrational response of the wing is equivalent to a sinusoidal excitation force, which is the inertial force. The dynamic motion given by Eq. (3-12) is coupled to the fluid motion via the fluid force term f*xt, which cannot be solved in a closed form due to its non-linearities.
For high-density-ratio FSI systems, Daniel and Combes [470] and Combes and Daniel [472] showed that the inertial force arising from the wing motion is larger than the fluid dynamic forces. To cover a wider range of density ratios, Kang et al. [351] included the fluid dynamic forces by considering the added mass effects. The motivation stems from the scaling discussed in Section 3.6.4, where for high к the added mass terms due to an accelerating body (see also Combes and Daniel [472]) contribute more on the wing than do the fluid dynamic forces from the hydrodynamic impulse; see Table 4.2 for a summary of the non-dimensional numbers considered in this study. Figure 3.55 illustrates the domain of importance of the various effects of the unsteady fluid force. Hence, the wing dynamics is modeled with external forces depending on the imposed wing acceleration as
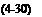 f*xt (t*) ^ 2п2St к cos(2nt*),
f*xt (t*) ^ 2п2St к cos(2nt*),
and the external force on the structural dynamics does not have spatial distribution explicitly accounted for and is being simplified in temporal form.
When dombined with the inertial force, the total external force g(t*) becomes
g(t*) = f*xt (t*) – П0 d h(l ) « 2п2 1 + — p*h* St к cos(2nt*). (4-31)
dt *2 п
The solution for the tip displacement is given by Kang et al. [351] who used the method of separation; that is, v* (x*, t*) = X(x*)T(t*) as
for the temporal component, with Qn, the Fourier coefficient of a unit function in the spatial modes, satisfying
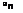 j XndX Xndx
j XndX Xndx
0
and the natural frequency
with kn as the eigenvalue belonging to the spatial mode Xn with k1L & 1.875. The spatial component Xn is the same as for a cantilevered oscillating beam. The temporal evolution of the wing given by Eq. (4-32) indicates there is an amplification factor of 1 /(f2/ f2 – 1), depending on the ratio between the natural frequency fn of the beam and the excitation frequency f.
The full solution is w*(x*, t*) = h(t*) + J2 n==1Xn (x*)Tn (t*). The amplitude of the tip deformation, у, for the first mode (n = 1) is given as
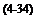 (1 + Пp*h* ■ st ■ k
(1 + Пp*h* ■ st ■ k
По (f2/ f2 – 1)
relative to the imposed rigid body motion normalized by the chord. The parameter Y can be rewritten as
 Y ( P^m ^ + Л 4_________ A + 1
Y ( P^m ^ + Л 4_________ A + 1
ha/cm pshs 4 f^2 – 1 – 1
where f1/ f = ш1 /(2n) is the inverse frequency ratio and A = npcm/(4pshs) is the ratio between the acceleration-reaction force (added mass) and the wing inertia. Depending on the order of this ratio, either the acceleration-reaction force term or the wing inertia force can be neglected. Equation (4-35) gives the relative wingtip deformation normalized by the plunge amplitude, which can be related to the Strouhal number based on the deformed tip displacement. Note that when A is sufficiently large, the inertia force term can be neglected and Y is then proportional to Ah* – pha/(pshs).
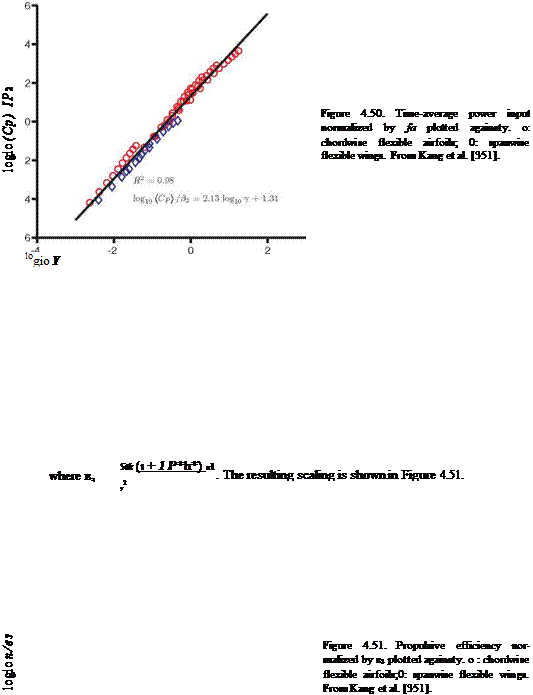
The proposed scaling parameter to estimate the resulting force on the flapping wing follows from the observation that there exists a correlation between the dynamic deformation of the wing at the tip, y , given by Eq. (4-34), and the static tip deflection, which is (CF) /Пг. By considering the non-dimensional energy equation, Kang et al. [351] derived the following relation between the time-averaged force [CfI and the maximum relative tip displacement represented with the scaling factor y, under the assumption of f1 / f < 1, resulting in
<Пг> – Y. (4-36)
П1
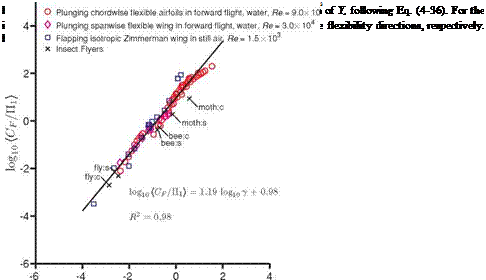
The resulting scaling – Eq. (4-36) for the three canonical cases – is shown in Figure 4.40. When plotted in the log-scale, see Figure 4.40, the scaling for all cases
considered becomes more evident. A linear fit on the data set with the coefficient of determination of R2 = 0.98 indicates that the relation between the normalized force and y is a power law with the exponent of 1.19. The relation originating from the dimensional analysis, Eq. (4-36), then simplifies to
[CF) = Ui^(y), (4-37)
with ^(y) = 10098y 119. The elastoinertial number, Nei proposed by Thiria and Godoy-Diana [454] as the thrust scaling parameter in air is a special case of y ; that is,
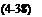
р*й;»1 and ///1»1
Y——————- ► Nei-
It is important to note that the у-axis in Figure 4.40 shows [CF). Recall that [CF) was defined as the force acting normal to the wing that is responsible for the wing deformation; hence [CF) is normal to [CT) or (CL) depending on the direction of the wing deformation. For the purely plunging chordwise flexible airfoil cases in forward flight in water, [CF) = [CT)/(St ■ k) where the factor St ■ к is the ratio between CL max/ [CT) ~ St ■ к for the added mass force and [CT] by Garrick [335] for purely plunging airfoils. For all chordwise flexible airfoil cases parametrized by (f, h*), (CF) /П1 shows almost a linear correlation with y. Recall that the inertial force term arising from the plunging boundary condition is small compared to the added mass term because for the plunging chordwise flexible airfoils p*h* < 1. Compared to the higher motion frequency cases, the thrust generation at the lowest frequency at the five thicknesses has a larger variance, which is not shown in Figure 4.40. A plausible explanation is that the current analysis breaks down due to the presence of the rigid teardrop at lower motion frequencies. When the plunging
motion is very slow at the rigid teardrop, the large leading-edge radius produces time-averaged drag that overwhelms the thrust generation from the thin flat plate with small deflection. The airfoil produces drag at St = 0.085 on all five thickness ratios as shown in Figure 4.40, which would result in an under-predicted value of
CL /П1.
For the spanwise flexible wing, although the Reynolds number and the thrust direction relative to the wing flexibility are different than in the chordwise flexible airfoil, a similar analysis could be made by approximating the three-dimensional wing as a beam with the correction factors l/cm = AR for П0 and П1 as discussed in Section 4.5. The force coefficient is scaled with the same parameters as for the chordwise flexible airfoils for the same reasons; that is, CL = CL/(St/к).
In the case of a flapping Zimmerman wing, the wing hovers in air, and so the density ratio is higher than in water. Hence, the inertial force dominates over the added mass force, as previously found [470] [472]. The horizontal force CL is found by normalizing CL by h* because the vertical force and the horizontal force are proportional to the thickness ratio, if we assume that the pressure differentials are of the order of 0(1). Furthermore, the computed lift from the numerical framework represents only the fluid dynamic force without the inertial force of the wing. The inertial force that acts on the wing is estimated by multiplying the factor p*h*/(St/к), which is the ratio between the inertial force (~ p *h*k2) and the fluid force (~ St к) to CL. The resulting normalization for the vertical axis is then CL = CL P*/(St/к).
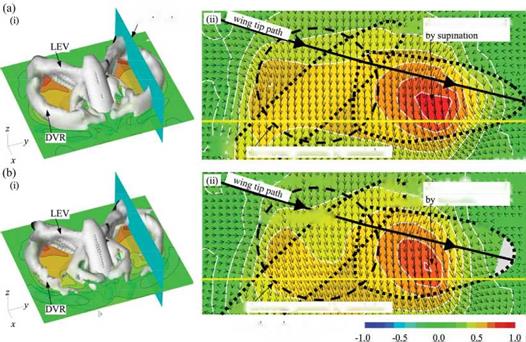
Even though the current case has different kinematics (plunging vs. flapping; forward flight vs. hovering), different density ratios (low vs. high), and structural flexibilities (unidirectional vs. isotropic), the previous trend reemerges, suggesting the generality of this scaling parameter у. The trend for the flapping isotropic Zimmerman wing hovering case is slightly offset in the vertical direction, suggesting that the resulting lift is lower. An important factor is the influence of the presence of the rigid triangle (see Figure 4.37) that constrains the tip deformation, such that the resulting tip deformation is less than in the setup where the imposed kinematics is actuated at the root of the wing without the rigid triangle.
For the flapping isotropic Zimmerman wing case in hovering motion, we could correlate the lift generation to y. This result suggests extrapolation of the current scaling analysis to the lift generation of hovering insect flyers. The lift in hovering motion for several insects is approximated by the experimentally measured weights of hawkmoths [226, 227], bumble bees [512], and fruit flies [513] [514]. To calculate the parameters listed in Table 4.3, a flapping rectangular planform has been assumed with constant thickness and density. To compute the effective stiffnesses in the spanwise and the chordwise directions (i. e. n1s and n1c, respectively), the flexural stiffness data presented by Combes and Daniel [402] were used along with their wing lengths. The result is included in Figure 4.42 with the scaling
Again, the lift approximated with the weights of the insects scales with y.
The current analysis shows that the time-averaged force, such as the thrust or lift, can be related to the maximum relative tip displacement by normalizing the
|
Insect
|
Hawkmoth
|
Bumble bee
|
Fruit fly
|
|
cm [mm]
|
18.2
|
3.22
|
0.96
|
|
R [mm]
|
47.3
|
10.9
|
3.0
|
|
f [Hz]
|
26.1
|
181
|
240
|
|
fa [deg.]
|
57.2
|
72
|
75
|
|
Re [103]
|
6.2
|
2.2
|
0.25
|
|
K
|
0.30
|
0.18
|
0.19
|
|
St
|
0.25
|
0.25
|
0.25
|
|
h* [10-3]
|
2.0
|
1.0
|
0.6
|
|
p* [103]
|
2.0
|
2.1
|
1.1
|
|
n1,s [102]
|
0.43
|
1.4
|
26
|
|
n1,c
|
0.53
|
2.8
|
211
|
|
Table 4.3. Kinematic, geometric, fluid, and structural parameters for the hawkmoth, bumble bee, and fruit fly obtained from the literature
|
|
Source: Willmott and Ellington [226] [227], Buchwald and Dudley [512], Vogel [513], Shevtsova et al. [514], and Combes and Daniel [402].
|
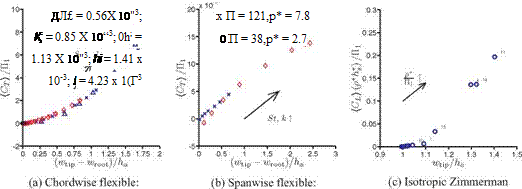
force by the effective stiffness, П1, resulting in a measure equivalent to the static tip displacement. These features are shown in Figure 4.41. Note that the relation is not linear, indicating that c in Eq. (4-34) is actually not a constant. For the spanwise flexible wing case, although the very flexible wing has larger relative deformation, the effective stiffness is 5.6 times smaller than that of the flexible wing. Hence even if the static tip displacement is larger for the very flexible wing at the highest motion frequency, the force corresponding to this deformation is smaller due to a lower effective stiffness. Furthermore, plotting the [Ct) /П1 against the maximum
Figure 4.41. Time-averaged force (thrust or lift) coefficient normalized by the effective stiffness plotted against the maximum relative tip deformations for the current computations. The numbers shown in (c) next to the markers indicate their case numbers. From Kang et al. [351].
relative tip deformation collapses both curves on top of each other. It is shown in Eq. (4-35) that for p*h* > 1 the inertial force will have greater influence on the wing deformation than the force due to added mass. In air, p* is high, so that in addition to the normalization by the effective stiffness, the time-averaged force needs to be multiplied by p*h* to account for the inertial force.
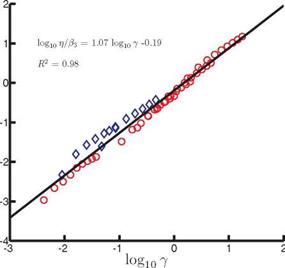
Without assuming that f / f1 < 1, Kang and Shyy [404] considered hovering motions of flexible flat plates at Re = 100 and 1,000. A sinusoidal plunging motion was imposed at the leading edge of the flat plate in a fluid with the density ratio of 7.8, corresponding to steel in water. The flat plate deformed under its own inertia and the resulting aerodynamic load, which led to passive pitch. The frequency ratios considered for this study were 0.04 < f / fi < 0.8. Applying the scaling given by Eq. (4-36) resulted in a non-monotonic trend for the higher frequency ratios, suggesting that Eq. (4-36) is indeed only valid for small frequency ratios. Instead, they proposed a revised scaling by approximating the wingtip velocity with 2nY, which led to
Eq. (4-40) was able to scale the lift generated by a hovering flexible flat plate
including passive pitch, where в1 = П^1 – ^ f j J. An interesting property of the
scaling given by Eq. (4-40) is that when f / f1 < 1, the denominator in the LHS becomes П1, resulting in Eq. (4-36).
In summary, the thrust generation consists of contributions from both leading – edge suction and the pressure projection of the chordwise deformed rear foil. When the rear foil’s flexibility increases, the thrust of the teardrop element decreases, as does the effective angle of attack. Within a certain range, as chordwise flexibility
increases, even though the effective angle of attack and the net aerodynamic force are reduced due to chordwise shape deformation, both mean and instantaneous thrust are enhanced due to the increase in the projected area normal to the flight trajectory. Furthermore, for the spanwise flexible case, correlations of the motion from the root to the tip play a role. Within a suitably selected range of spanwise flexibility, the effective angle of attack and thrust forces of a plunging wing are enhanced due to the wing deformations.



















 f % t * ** *■ * < < < * * ^
f % t * ** *■ * < < < * * ^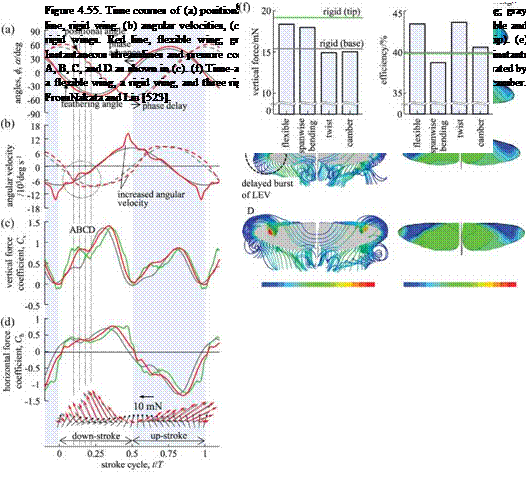

 El: flexural stiffness
El: flexural stiffness
 Polyester film
Polyester film
![Подпись: Force 119 Efficiency в3у117 Source: [351].](/img/3131/image520_2.gif)


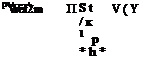
![Подпись: log Y aio ' Figure 4.42. Normalized time-averaged force coefficients as function of Y, following Eq. (4-40). The data points for the forward flight cases, the Zimmerman wing cases, and the insects are the same as in Figure 4.40. From Kang and Shyy [359].](/img/3131/image477_2.gif)