LAPLACE AND FOURIER TRANSFORMS

The quantities with which we have to deal in physical situations usually turn up naturally as functions of space and time. For example, the state or motion of a flight vehicle is a function of time, and the velocity of the atmos­phere is a function of three space coordinates and time. It has been found to be very advantageous in many problems of analysis to abandon this “natural” form of the functions, and to work instead with certain “integral transforms” of them.

о

Table 2.1 Fourier Series Fourier Integral® Fourier Transform® One-Sided Laplace Transform x(t) defined in domain — T<t <T — CO < t < 00 — 00 < t < 00 0 < 2 < oo Transform a> CT Cn = —2 x(t)e-inaa* dt 2W J_T V’ if” . , C(<o) = — x(t)<rxatdt 277 J_oo Лео Х(ш) = x(t)e-iat dt J — 00 JS?[®(t)] = *(e) Лео = і x{t)e~si dt (2.3,1) (2.3,3) (2.3,5) Jo (2.3,7) Inverse 00 x(t) = 2 Oneina0( 71——00 Лео x(t) = I C(a>)eimt dm J— oo if" . , x(t) = — Х(со)е«°* dco 277 J-.о x{t) = — I x(s)est ds 2777 Jc (2.3,2) (2.3,4) (2.3,6) (2.3,8)

а No real distinction is made in the literature between Fourier integrals and Fourier transforms. The convention adopted here makes the inverse of the former the limit of the Fourier series as T —► со, and the latter a special case of the one-sided Laplace transform in which the domain is altered and s is imaginary.

DEFINITIONS

Table 2.1 presents the common one-dimensional transforms of a function x(t) and the companion “inversion formulae” or “reciprocal relations” that give the “natural” function in terms of its transform.

Multidimensional transforms are formed by successive application of these operations. (An example of this is given in Chapter 13.)

Before proceeding further with the discussion of Table 2.1, it is expedient to introduce here the step and impulse functions, which occur in the following tables of transforms.

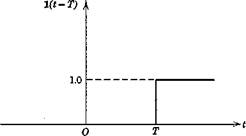
The unit step function is (see Pig. 2.1)

x(t) = l(t – T) (2.3,9)

Fig. 2.1 Unit step function.

It has the values

x(t) = 0, t < T

x{t) = 1, t > T

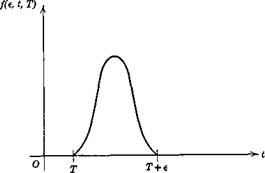
The impulse function or delta function (more properly, the Dirac “dis­tribution”) (see Fig. 2.2) is defined to bef

d(t — T)— lim/(e, t, T) (2.3,10)

£->0

where /(є, t, T) is for є > 0 a continuous function having the value zero except in the interval T <t < T + e and such that its integral is unity, i. e.

pT+e

I f(e, t,T)dt= 1

t The limit in (2.3,10) has a rigorous meaning in the sense of distributions, despite the fact that it does not exist in the classical sense.

Fig. 2.2 The impulse function.

It follows that

j*d(* — T)dt = 1 (t – T) (2.3,11)

and hence that

d(t — T) — — l(t — T) dt

When the T is omitted from (2.3,9) and (2.3,10) it is assumed to be zero (as in Table 2.2, item 2).

Some Fourier Transform Pairs

Table 2.2 x(t) X(a>) 1 6(t – T) е~іюТ 2 <5 (t) 1 3 QiCit 2тг <5 (to — 4 1 2-n – d(c«) 5 cos €lt 7т[в(а> + П) + в (со – П)] 6 sin. Ctt •ітг[<5 (<о + Q) — <5(со — £1)] 7 І sgn t 1 ІОІ 8 1(0 — + 7Г (5(ft>) ісо

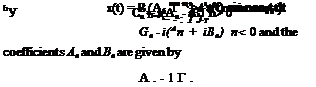In the first column of Table 2.1 is given the complex form of the Fourier series for describing a function in the finite range — T to T, in terms of fundamental circular frequency eo0 = 77jT. The coefficients Gn are related to those of the real Fourier series

The amplitude of the spectral component of frequency nm0 is

(AJ + B*)* = 2 IGn (e)

When T —*■ oo, the Fourier series representation of a function x(t) passes over formally to the Fourier integral representation, as given in the second column. In this limiting process

№со0->ш, and C( <x>) = lim — (2.3,13)

<ao~*0 COq

The Fourier transform that follows in the third column is essentially the same as the Fourier integral, with trivial differences in notation and the factor 1/2тг. In some definitions, both the transform and its inverse have the factor l//2 77. Some useful Fourier transforms are presented in Table 2.2.

From one mathematical viewpoint, C(w) and -X(co) do not exist as point functions of to for functions x(t) that do not vanish at 00. This is evidently the case for items 3 to 8 of Table 2.2. However, from the theory of distri­butions, these transform pairs, some of which contain the singular <5 function, are valid ones (see ref. 2.3). Items 1 and 2 are easily verified by substituting x(t) into (2.3,5) and items 3 to 6 by substituting X(a>) into (2.3,6). Formal integration of x(t) in item 7 produces the X(oi) shown plus a periodic term of infinite frequency. The latter has no effect on the integral of X(a>), which over any range dm > 0 is (I/t’co) dm. Item 8 is obtained by adding item 7 to of item 4. The one-sided Laplace transform, in the fourth column of Table 2.1, is seen to differ from the Fourier transform in the domain of t and in the fact that the complex number s replaces the imaginary number im.

The two notations shown in (2.3,7) are used interchangeably. The curve c on which the line integral is taken in the inverse Laplace transform (2.3,8) is an infinite line parallel to the imaginary axis and lying to the right of all the poles of 2(a). If its poles all lie in the left half-plane then c may be the imagi­nary axis and (2.3,8) reduces exactly to (2.3,6).