Physics of Aerodynamic Flows

This chapter will describe the properties of atmospheric air, summarize key physical relations between these properties, and derive the equations of fluid motion which form the basis of aerodynamics.

1.1 Atmospheric Properties

A typical dimension t of any common aircraft is vastly greater than the molecular mean free path A of the air at any practical operating altitude, as quantified by the Knudsen number Kn = A/t ^ 1. Consequently the air can be considered to be a continuum fluid having a density p, pressure p, temperature T, and speed of sound a at every point in space and time. There are also viscous stresses and heat conduction at each point, which are quantified by the fluid’s viscosity p and heat conductivity k. The US Standard Atmosphere [1] has the following values for these properties for air at sea level.

density:	pSL	= 1.225 kg/m3
pressure:	pSL	= 1.0132 x 105 Pa
temperature:	Tsl	= 288.15 K	(1.1)
speed of sound:	aSL	= 340.3 m/s
viscosity:	pSL	= 1.79 x 10-5 kg/m-s

Reference [1] also gives equations for these quantities at other altitudes, and tabulated values are also avail­able from many sources. Alternatively, the following curve-fit formulas for the pressure and temperature may be more convenient for numerical work, with the altitude z in kilometers and temperatures in Kelvin.

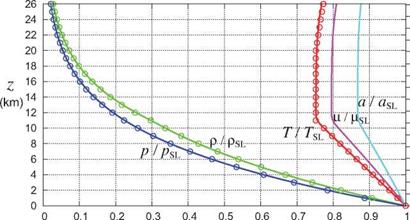
These approximations are accurate for z< 47 km, and are shown in Figure 1.1 for z< 26 km.

With p(z) and T(z) known, the atmospheric density p(z) can then be obtained from the ideal gas law (1.7), and the speed of sound can be obtained from expression (1.70) given in Section 1.7.3. The viscosity is accurately given by Sutherland’s Law with TS = 110 K for air,

which can also be used to relate the local viscosity to the local temperature at any point in a flow-field.

For gases, the heat conductivity k can be most easily obtained from the viscosity via the Prandtl number, Pr = cp p/k, which is very nearly constant across a wide range of temperatures. The specific heat cp will

80 70

60

50 Z (kft) 40v ‘

30

20 10

0

Figure 1.1: Atmospheric properties versus altitude, relative to sea-level values. Symbols are from the US Standard Atmosphere. Lines are curve fits (1.2), (1.3), and gas relations (1.4), (1.7), (1.70).

be defined in the next section.

k = Op p/Pr (1.5)

Pr = 0.72 (for air) (1.6)