Stability, Control, and Equilibrium

It is appropriate here to define what is meant by the terms stability and control. To do so requires that we begin with the concept of equilibrium.

A body is in equilibrium when it is at rest or in uniform motion (i. e., has constant linear and angular momenta). The most familiar examples of equilibrium are the static ones; that is, bodies at rest. The equilibrium of an airplane in flight, however, is of the second kind; that is, uniform motion. Because the aerodynamic forces are de­pendent on the angular orientation of the airplane relative to its flight path, and be­cause the resultant of them must exactly balance its weight, the equilibrium state is without rotation; that is, it is a motion of rectilinear translation.

Stability, or the lack of it, is a property of an equilibrium state.[2] The equilibrium is stable if, when the body is slightly disturbed in any of its degrees of freedom, it re­turns ultimately to its initial state. This is illustrated in Fig. 1.3a. The remaining sketches of Fig. 1.3 show neutral and unstable equilibrium. That in Fig. 1.3d is a more complex kind than that in Fig. 1.3b in that the ball is stable with respect to dis­placement in the у direction, but unstable with respect to x displacements. This has its counterpart in the airplane, which may be stable with respect to one degree of free­dom and unstable with respect to another. Two kinds of instability are of interest in

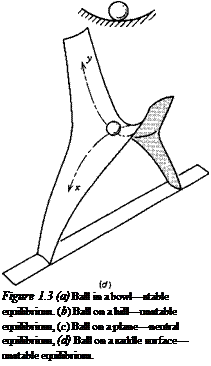airplane dynamics. In the first, called static instability, the body departs continuously from its equilibrium condition. That is how the ball in Fig. 13b would behave if dis­turbed. The second, called dynamic instability, is a more complicated phenomenon in which the body oscillates about its equilibrium condition with ever-increasing ampli­tude.

When applying the concept of stability to airplanes, there are two classes that must be considered—inherent stability and synthetic stability. The discussion of the previous paragraph implicitly dealt with inherent stability, which is a property of the basic airframe with either fixed or free controls, that is, control-fixed stability or control-free stability. On the other hand, synthetic stability is that provided by an au­tomatic flight control system (AFCS) and vanishes if the control system fails. Such automatic control systems are capable of stabilizing an inherently unstable airplane, or simply improving its stability with what is known as stability augmentation sys­tems (SAS). The question of how much to rely on such systems to make an airplane flyable entails a trade-off among weight, cost, reliability, and safety. If the SAS works most of the time, and if the airplane can be controlled and landed after it has failed, albeit with diminished handling qualities, then poor inherent stability may be acceptable. Current aviation technology shows an increasing acceptance of SAS in all classes of airplanes.

If the airplane is controlled by a human pilot, some mild inherent instability can be tolerated, if it is something the pilot can control, such as a slow divergence. (Un­stable bicycles have long been ridden by humans!). On the other hand, there is no
margin for error when the airplane is under the control of an autopilot, for then the closed loop system must be stable in its response to atmospheric disturbances and to commands that come from a navigation system.

In addition to the role controls play in stabilizing an airplane, there are two oth­ers that are important. The first is to fix or to change the equilibrium condition (speed or angle of climb). An adequate control must be powerful enough to produce the whole range of equilibrium states of which the airplane is capable from a perfor­mance standpoint. The dynamics of the transition from one equilibrium state to an­other are of interest and are closely related to stability. The second function of the control is to produce nonequilibrium, or accelerated motions; that is, maneuvers. These may be steady states in which the forces and accelerations are constant when viewed from a reference frame fixed to the airplane (for example, a steady turn), or they may be transient states. Investigations of the transition from equilibrium to a nonequilibrium steady state, or from one maneuvering steady state to another, form part of the subject matter of airplane control. Very large aerodynamic forces may act on the airplane when it maneuvers—a knowledge of these forces is required for the proper design of the structure.

RESPONSE TO ATMOSPHERIC TURBULENCE

A topic that belongs in dynamics of flight and that is closely related to stability is the response of the airplane to wind gradients and atmospheric turbulence (Etkin, 1981). This response is important from several points of view. It has a strong bearing on the adequacy of the structure, on the safety of landing and take-off, on the acceptability of the airplane as a passenger transport, and on its accuracy as a gun or bombing plat­form.