Uncertainties Induced by the Grid Topology

The intention of this study was to analyse the influence of the grid topology on the flow solution. For this purpose a set of four grids was generated. Both trailing- edge variants were discretized in c – and o-shape as shown in Figure 3. Numerical simulations were conducted at Re = 4 • 106, Ma = 0.1. The angle of attack was varied from a = 4° to 14° in steps of two degrees. As closure conditions for the RANS-equations the turbulence model according to Spalart-Almaras has been used. For the c-type grids a grid convergence study was conducted. For this purpose two additional grids were generated by unified coarsening and refinement of the initial grid. The polar curve in Figure 4 shows the result of this study. It compares the corresponding solutions on the c – and o-grids. The polar curves reveal that the grid topology has a significant influence on the aerodynamic coefficients. The variation of the grid topology for the blunt trailing edge yields a variation of about 4.0 to

7.0 drag counts. For the airfoil with the sharp trailing edge the differences vary from 2.50 to 5.50 drag counts. In addition, the differences in cl and cd decrease with growing angle of attack for the blunt trailing-edge case. For the airfoil with the sharp trailing-edge no such behaviour is visible.

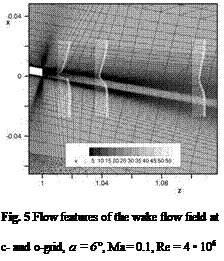
Analysing the flow solution around the trailing edge is advisable to understand this behaviour. For this purpose Figure 5 shows a detailed plot of the flow solu­tion around the trailing edge at a = 6°. Solutions obtained on c- and o – grids are compared. In addition, the wake velocity profile downstream of the trailing edge is shown at three slices. As one can see, there are significant differences between the two solutions. Unlike the o-grid, the c-grid can capture the wake velocity pro­file and the flow field gradients very well and can preserve them far downstream. The o-grid shows a strong dissipation of the flow features. This can be attributed to the coarse wake discretization on this o-grid. The same statements are valid on c – and o-grids with sharp trailing edges. The variation of topologies mainly shows an

effect on cd. The effect on c is negligible for attached flows and for flows with small trailing-edge separations.

These results show that meshing trailing edges in o-type topology can be prob­lematic. In general, o-type grids lead to a quick coarsening of the grid downstream of the trailing edge. Especially on airfoils with sharp trailing edges, this coarsen­ing effect is very strong. To reduce this coarsening for o-grids with blunt trailing edges, the number of grid points at the trailing edge has to be increased, whereas for sharp airfoils more grid points have to be shifted towards the trailing edge. However, compared to a c-grid this still does not yield a satisfying solution, since a reasonable resolution of the flow field downstream the trailing edge cannot be achieved even after excessively increasing the number of grid points. The finding, that changing the grid topology has a bigger impact on the flow solution than a change in the trailing-edge geometry is an important conclusion of this analysis.

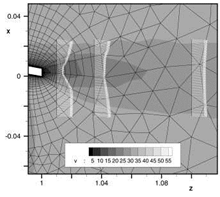Fig. 4 Influence of different grid topologies and grid resolutions on c and q of the NLF(0)416 airfoil with different trailing edge geometries at Ma = 0.1, Re = 4 • 106

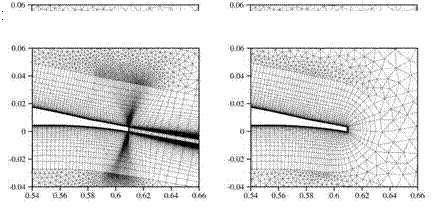
(a) c-grid, blunt trailing edge (b) o-grid, blunt trailing edge