Analysis Methodology

Since one of the aims of this work was to study the infbence of the torsion centre for different reduced frequencies and configurations it was decided to follow a simplified design approach (Panovski and Kielb, 2000). The basic

Figure 2. Description of the blade motion as a rigid body

idea is to assume that the main contribution to the aerodynamic damping is due to the actual blade and the two neighbouring blades. In this case the aero­dynamic damping varies sinusoidally with the inter-blade phase angle and it may be computed with as few as three linear computations. The validity of such approach has been shown both experimentally (Nowinski and Panovski, 2000) and numerically (Panovski and Kielb, 2000).

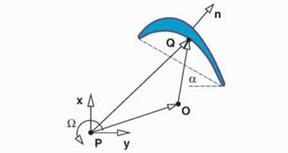
Following the approach of Panovski and Kielb (2000) just the unsteady pres­sure field associated to the bending in the x and y direction and the torsion about a given point, P, for a reference displacement are computed. The un­steady pressure associated to the motion of the airfoil as a rigid body about an arbitrary torsion axis, O, is computed as a linear combination of three refer­ence solutions. The velocity of an arbitrary point, Vq, of the airfoil is of the form:

Vq(t) = Vp(t) + fi(t)k x PQ (7)

where fi is the angular velocity of the airfoil, k is the unit vector perpendicular to the xy plane. Choosing VP and fi properly it is possible to make an arbitrary point O the torsion axis, this condition is

Vo(t) = Vp(t) + fi(t)k x PO = 0 (8)

and hence is enough to satisfy Vp = —fik x PO for an arbitrary fi. We may write Vp = vx i + vyj where

vx = exwRe [ihx, ref elwtj and vy = eywRe (ihy>ref elwtj (9)

and ex and ry are scaling factors of the actual displacements with respect the ones of reference hx ref and hy, ref. Analogously

a = r^Re (aref elut) and fi = r^wRe (iaref elut) .

The unsteady pressure perturbation, p due to the motion of the airfoil as a rigid body is assumed to behave linearly and therefore it may be expressed as the sum of the unsteady pressure fields associated to bending in the x direction, p’Vx, bending in the у direction, p’ , and torsion about the point P, p’n, i. e.:

Pf = Pvx + Pvy + Pn = exPvx, ref + eyPvy, ref + enPn, ref – (H) The work per cycle over the airfoil, W, is

р2тг/и r

w= / p’Vq. dAdt (12)

Jo Jy, c

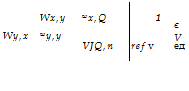where is the velocity of the blade surface. W > 0 means that the blade motion is damped by the aerodynamics. Substituting equations 7 and 11 in 12 it is possible to obtain the following expression for W in non-dimensional form:

where each element of work coefficient matrix represents the non-dimensional work obtained combining each unsteady pressure field with on the displace­ments of each mode (e. g. wx^ is the work perform by the unsteady pressure associated to the airfoil bending in x on the displacements due to the torsion about point P), pe and Ue are, respectively, the density and velocity at the cas­cade exit, dmax is the maximum airfoil displacement in the reference cases and cH is an estimate for the airfoil surface.

The work coefficient matrix [w] is calculated once for each IB FA of the fun­damental modes. The general procedure is then to run the unsteady code in the three fundamental modes with a reference amplitude through the range of inter-blade phase angles. As few as three inter-blade phase angles per funda­mental mode need to be used. The rest of IB FA are obtained assuming that w = a + b sin a + c cos a. The critical IB FA is computed then as the minimum of the previous expression.

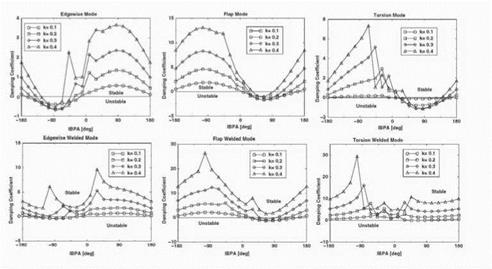
In this work we have obtained the values of the damping coefficients for a = 0° and a = ±90° to estimate the whole range of inter-blade phase angles. The errors associated to this approximation may be seen in figure 3 where the damping coefficients for the edgewise, fhp and torsion modes for different reduced frequencies are displayed. It may be appreciated that the damping coefficient curves of the edgewise and fhp modes have a sinusoidal form. This is specially true for к = 0.1 while for к = 0.4 two spikes, corresponding to resonant conditions, are superimposed to the sine-like shape. This behaviour

Figure 3. Damping as a function of IBPA for the three fundamental modes. Top: single blade configuration. Bottom: Welded-pair configuration

is as could be expected since it is well known that the relative inflience of the adjacent blades to the reference one decreases when the reduced frequency is increased (see Corral & Gisbert (2002) for example). The deviations from the sinusoidal from of the torsion mode are larger, but in all the cases the critical interblade phase angle is still well predicted.