Free space Green’s function and integral formulation

Using the superposition principle we obtain an integral formulation of the wave equation for free space conditions. We first consider the sound generated by a pulse from a point source. This implies a localization in time and space, obtained by using the delta function. The delta function S(t) is a generalized function defined by [Chrighton (1992)]:

/

TO

5(t)f (t)dt = f (0)

-TO

For any well behaving function f(t) and:

5(t)dt = 1

The delta function has no meaning outside an integral. The free-field Green function Go(x, ty, T) is the solution of the wave equation:

1 d2 Go ^ ~W
V2Go
S(t — t)S(x — y)	(71)

where S(x — y) = 5(x — y)5(x2 — y2)S(x3 — y3), for free-field boundary conditions and for the initial conditions:

Go(x, ty, T) = 0, t < t

and

d — Go(x, ty, T)=0, t < t

(73)

corresponding to the causality condition that a wave cannot reach an ob­server before it has been emitted. In order to determine G0(x, ty, t) we use the Fourier transform G0 defined by:

Go(x, ty, T)	Go(u, xy) exp(iwt)dw	(74)

and

Go(w, xy) = — Go(x, ty, T)exp(-iwt)dt.

2n.1^,

As we consider the field generated by a point source in free-field conditions we know that the Fourier transform of the Green function is given by:

л A

Go(u, xy) = — exp(—ikr)

where A is an amplitude which will be determined by using the properties of the delta function. We take the Fourier transform of the wave equation (71). Using the property (69) of the delta function:

2П f-oo S(t — T) exp(—i^t)dt =

(77)

= 2П f-o-r 6(t – T) exp(-iw(t – T) – ІШТ)d(t — T) = ЄХРІ2ПШТ}

we find:

— (k2 + V2)Go = ^Z! A. (78)

2П

We integrate this equation over a spherical volume V of radius R enclosing the source:

-f (k2 + V2)GodV = exp(~^T) . (79)

Jv

By taking the limit of a compact control volume kR << 1 and using the Gaussian Theorem we find:

which yields the amplitude A. Substituting A in (76) and transforming back to the time domain yields:

Go(x, ty, T )= ^(T4-rtg) (81)

where the emission (retarded) time te is defined by:

r

te = t——– . (82)

co

Because Green’s function in free-space only depends on the distance r and time difference (t — t), rather than on the source and observer’s coordinates (x, t) and (y, T) separately, it satisfies the important symmetry properties:

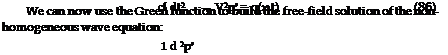
Equation (83) is the so-called reciprocity relation, which is also valid for Green’s functions in the presence of walls.

by using the superposition principle:

Substitution of (87) into (86) and using the definition (71) of Green’s function we can verify the validity of this solution.

In the presence of walls, we can still use the same free-field Green func­tion. However, now the solution of the wave equation will include surface integrals representing the effect of reflections of waves at the walls. Using Green’s theorem we have:

p'(x, t)= J—oo Uq(y, T )Go(x, ty, T )dVydr (88)

— I-o Is [p’vyGo — GoVyp’J ■ ndSydr. ( )

This integral formulation, in combination with Lighthill’s analogy, yields the integral formulation of Curle (1955). The control volume is chosen such that it encloses the observation point x. Note that in the literature the sign of the unit normal n is often chosen to be the opposite of the sign chosen here [Goldstein (1976), Dowling and Ffowcs Williams (1983)].

An alternative approach is the use of a so-called tailored Green function [Dowling and Ffowcs Williams (1983)]. This is a Green function defined by the wave equation (71) and the same (locally reacting linear) boundary conditions as the acoustic field under consideration. In that case the surface integrals of (88) vanish. An example of such a Green function for the trailing edge of a plate will be discussed in later chapters, Part 2.

1.4 Monopole, dipole and quadrupole

We consider radiation of a spatially limited source-region under free field conditions. Whenever the source region (q(x, t) = 0) is compact, we can ne­glect variations in the retarded time te in the integral of equation (87).

Choosing the origin within the source region we get at distances large com­pared to the source region:

r = x — f* x (89)

so that we have:

P'(xX<> * XjX X — Xі dV

We call the integral fV q y, t — dVy the monopole strength of the source

region. Whenever the source is the divergence of a force field q(x, t) = —V-f integral (91) taken over a volume including the source region will vanish because the surface integral of the flux of the force field fS f • ndSy = 0 vanishes because f = 0 on the surface. The surface, including the control volume, is outside the source region so that the force is either uniform or zero. By partial integration and using the symmetry property (83) we can write the formal solution of the wave equation as:

p’(x, t) = — /-w fV(Vy • f(y, t))Go(x, ty, T)dVydr

= — /-^ fV f(y, r)VxGo(x, ty, T)dVydr.

As the integration over the source coordinates f does not interfere with the derivation by observer’s coordinates x we have:

p!(x, t) = —Vx •[ ( f(f, T )Go(x, ty, T )dVy dr. (93)

J-wJ V

For a compact source (kf << 1 and distances large compared to the dimension of the source region (x >> f), we have a dipole field:

p'(xt> *—Vx – (4ПХ X — f) ^ <94>

wher^ ^Jv f y, t — dVyj is the dipole strength.

An alternative way to find this expression is to consider the solution фі of the wave equation:

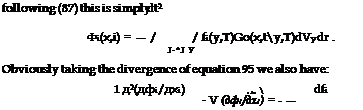which leads to equation (93) because p'(x, t) = —V • ф.

While a monopole can be represented as a pulsating compact sphere, a dipole field is generated by a compact translating sphere. In a similar way we can obtain for the sound source found in the analogy of Lighthill:

In a compact source region this is a so-called quadrupole field.

An alternative approach to the multipole expansion of the source [Gold­stein (1976)] is to use a Taylor series expansion of the free space Green function around y = 0 in the general solution (87):

which, using the symmetry properties (85) of the Green’s function and the far field approximation, yields:

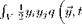dVy і…

(100)

An intuitive interpretation of monopole, diopole and quadrupole on surface water waves is provided in Figure 4. Due to the oscillating momentum in the region between the two monopoles forming a dipole it is obvious that a dipole cannot exist without any force acting on the fluid. This force is needed to change the momentum. Thus, unsteady force induces a dipole radiation and a dipole radiation cannot exist without a force acting on the fluid.