Quantification and Reduction of Numerical Uncertainties by Improvement of the TAU Grid Adaptation Tool and Adjoint Methods

Matthias Orlt and Nicolas R. Gauger

Abstract. Within the framework of the project MUNA, several enhancements of the grid adaptation tool of the DLR TAU Code were prepared, implemented and tested. Therefore, various quality aspects of the single elements of the computational grid were investigated and used to modify the adapted grids.

Conditions for the decomposability of the elements are evaluated and used for a more accurate compliance of the point density with the requirement of the error indicator in the grid refinement. Geometrical element quality terms for the element types of the TAU Code are derived from the known mean-ratio element quality meas­ure for a simplex and used to avoid the worst shaped elements in an adapted grid.

In addition, the TAU adaptation was extended to use the sensors provided by the adjoint solver of TAU as an error indicator for a goal orientated grid adaptation. The results are compared to that of a simple differences-based grid adaptation.

Furthermore, the adjoint method was used for the efficient quantification of un­certainties in the aerodynamic coefficients caused by variations of the parameters of the SAE and the Wilcox-k-m turbulence model.

1 Introduction

The goal of any grid adaptation in the solution of partial differential equations is to achieve the highest possible accuracy with the lowest possible effort. Under the assumption that the largest local discretization error affects the solution, the best one can do is to equidistribute the discretization error. So grid adaptation has two main

Matthias Orlt

German Aerospace Center (DLR), Institute of Aerodynamics and Flow Technology, C2A2S2E, Bunsenstr. 10, D-37073 Gottingen, Germany e-mail: matthias. orlt@dlr. de

Nicolas R. Gauger

Head of Computational Mathematics Group, Department of Mathematics and

Center for Computational Engineering Science (CCES), RWTH Aachen, (formerly DLR)

e-mail: gauger@mathcces. rwth-aachen. de

B. Eisfeld et al. (Eds.): Management & Minimisation of Uncert. & Errors, NNFM 122, pp. 29-53. DOI: 10.1007/978-3-642-36185-2_2 © Springer-Verlag Berlin Heidelberg 2013

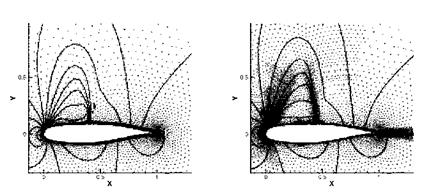
Fig. 1 Example of a grid adaptation around an airfoil, showing the initial grid (left) and the twice adapted grid (right) with different refinement levels and bridging elements between them

steps. The local discretization error is estimated and then the point density is changed. In areas with larger local errors the point density is increased and vice versa.

The TAU adaptation [1] is basically a hierarchical grid re – and derefinement using a special variant of the red-green-method and it works edge orientated. This means edge indicators are determined as numbers specifying the necessity to be refined or derefined for each edge. Depending on the available resources, i. e. a target point number, points are added to or removed from edges. In order to build a new grid from the new points some elements have to be subdivided and some have to be recomposed according to subdivided or rejoined edges.

The advantage of this method is, that it is fast compared to a local remeshing and that it can very accurately fulfill the edge indicator requirements. On the other hand a lot of elements are not refined completely because some refinements have to bridge between various refinement levels in order to get a conform adapted grid. Additionally, the refined area can be very scattered over the grid. This leads to even more bridging elements or nonregular refinements, see Fig. 1.

In order to preserve the semistructured character of the grid near walls in hybrid grids, the vertical edges of the prisms or hexahedra in layers are not subdivided. In areas with chopping, the vertical edges are edges of unstructured elements, too. If such elements are refined it has to be done nonregularly. Moreover there are some­times badly shaped elements which cannot be refined at all because even a regular refinement would lead to elements which cannot be split into positive tetrahedra parts for the dual computational grid of the TAU solver [11]. Especially large grids for complex geometries tend to include some of such elements, mostly with non­planar quadrilaterals.

The problem of refinement restrictions in conjunction with the element shape around unrefinable edges is addressed in the next Section 2 under the term element decomposibility. In this topic, the investigation of the geometric conditions for the validity of resulting elements enabled for an improvement of the edge refinement algorithm and led to a better compliance of point distribution with the requirements of the error indicator in the adapted grids.

In most cases, the element quality in terms of edge length relation and inner angles of the nonregular bridging refinements is lower than for the corresponding regular refinement. The following Section 3 deals with the element shape of bridging refinements under the term of geometrical element quality. Appropriate element quality measures were derived for the element types used in the TAU Code. After a second modification, the TAU adaptation got the option to avoid the nonregular subdivision of badly shaped elements in order to limit the worsening of the element quality in conjunction with bridging refinements.

The last topic is the use of the results of the adjoint solver as a sensor for the edge indicator of mesh adaptation. Furthermore, the adjoint method is used for the efficient quantification of uncertainties in the aerodynamic coefficients caused by variations of the parameters of the SAE and the Wilcox-k-ю turbulence model. For a description of the work at the adjoint solver and the possibility to consider parts of its results as an error estimator we refer to Section 4. The TAU adaptation related work at this point made the adjoint-based sensor available for the internal edge indicator and enabled for an adjoint-based adaptation. Some first tests were done within the project. They are presented and discussed in Section 5.

The three modifications include a better error indication, a more accurate adapt­ation to the required point density and a check of the geometrical element quality. Each of them aims at the reduction of the numerical uncertainty.