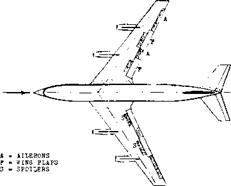
AIRPLANE PERFORMANCE

Methods of performance determination, such as finding the takeoff distance and rate of climb are not the purpose of this book. To point up the significance of certain aerodynamic characteristics that influence the design and selection of the various components of the airplane, some important principles of performance are presented, how­ever. These will include the primary design flight condi­tions of the airplane such as takeoff, cruise, high speed and landing. For more complete analysis of aircraft per­formance there are many excellent sources available (20).

Takeoff. The takeoff performance of an airplane, field length and distance over an obstacle, is directly influenced by the thrust, weight, CLX and drag. To accelerate the aircraft to the takeoff speed, high thrust to weight ratios are needed with a low drag to lift ratio. The speed at takeoff is a function of the maximum lift at the selected flap angle and the wing loading. In the case of large aircraft the rules for safety effectively determine the takeoff distance. As a result, the rate of climb with one failed engine at takeoff speed may be specified and be the determining factor. This is discussed in Chapter VI and determines the lift drag ratio at takeoff as well as the takeoff flap angle setting. The flap angle setting then establishes the lift coefficient at the takeoff speed which is usually

CL (at takeoff) = CLx/1.44 (45)

where Cux is maximum lift coefficient, the airplane in the takeoff configuration with the flaps at the proper angle and the landing gear down.

Climb and Descent. The rate of climb or descent is de­pendent on the difference in power available or required, the weight, velocity and the drag. Thus [12]

Equation 46 shows that a high lift drag ratio is required for a high rate of climb. High rates of descent are obtained at low lift drag ratios and at low or negative thrust conditions. Thus drag spoilers and thrust reversers are sometimes used to achieve high descent rates.

Takeoff Figure of Merit. Since both the distance and steepness of climb after takeoff are important the relative performance can only be judged by a factor that takes both the CL for takeoff and the rate of climb into effect. This may be done by finding the maximum rate of climb after takeoff at a minimum flight speed. Since for a given engine

wc /V = T/W – D/L = С, г С о /CL (47)

since V at takeoff is V ~ /C~L we can establish a figure of merit for takeoff as

FMto-(£ /СІ (48)

When the FMto is a minimum the angle of climb is a maximum. This factor gives an initial indication of the relative performance of different systems.

High Speed is basically made possible by reducing the drag coefficient of an airplane increasing thrust and by flying at higher altitude (in air with lower density). There are some effects, however, resulting from lift to be mentioned here:

a) Leading-edge devices such as slats in particular, are likely to precipitate turbulent boundary-layer flow, be­cause of the gaps and sheet-metal edges left when closed.

b) Not only the gaps of the trailing-edge flaps and ailerons, but also the arms or tracks supporting, and the devices deflecting them, are bound to contribute to drag.

c) A twisted wing can have a considerable amount of induced drag, even at zero total lift.

d) The horizontal tail surface may be loaded down at high speed, thus producing its own double trailing-vortex sys­tem, and making a higher lift coefficient necessary in the wing.

e) When flying at higher altitude, lift and induced-drag coefficients are necessarily increased. The induced drag (in newtons or pounds) might remain unchanged, however.

(22) Lifting characteristics of birds:

a) Lilienthal, ‘’Bird Flight and Aviation”, Translation London 1911.

b) Holst and Kuchemann, Probleme des Tierfluges, Natur – wi’schaften 1941 p 348.

c) Holst and Zimmer, Vogelflug, J. Ornithology 1943 p 371 & 406.

Drag and Lift**An airplane operating characteristics are determined according to its mass or weight, thrust or drag, and speed. So, while in the rest of this book almost nothing but coefficients are presented, ratios and meters per second are plotted as for example in figure 10. Drag consists of two components. The first, the ‘Viscous” or parasite drag is essentially proportional to the dynamic pressure q = 0.5 f V2. Thus

D0 = CDOTS (0.5 f V2) – ? V2 – vp2

In order to be independent of altitude and density, the “equivalent” airspeed is useful, that is the value “indi­cated” by an airspeed indicator calibrated for sea level density.

where (2 Wlf0 S) = constant for a given airplane in steady flight, without fuel consumption (and disregarding com­pressibility). The dynamic pressure is then

q = 0.5 fcVe =V//16

in ( kg /m-s2) = (N/me)

where f0 has a standard value (- in kg/m3, as in figure 3) and Ve in m/s. The second component of drag is that due to lift. The major portion of this drag is the induced drag. To account for some viscous drag originating as a conse­quence of lift, Oswald (20,a) has introduced a span – efficiency factor which we will designate by a. The drag due to lift:

Ц; = W21 Tf q a b = К (m/Ve b)

in (N = kg-m/s2′) (50)

where m = mass of the airplane (in kg). As a rule of thumb, ЛС0 = 0.01 , so that for A = 6, Д CD /С ql =

20%. For statistical purposes, then a = 1/1.2, and

К = 2 g2/^ f>0 a = 60 = constant

in (m5 /kg-s* ) (51)

Speeds. In terms of the indicated or equivalent speed, me lift of an airplane is

L = (W/ = mg = CL qS = CL 0.5 f0VeZS (52)

The speed corresponding to a given lift coefficient is accordingly:

V = vf2g/ )(m/SC~) =

4 /gm/SC in (m/s) 0 !)

where (m/S) in (kg/m2) = mass loading of the airplane and ^2g[f0 = 4 Vg = constant, in (m^/s^-kg). Considering now a sailplane in calm air (without any supporting up­wind) its “effective” (reduced to sea level) sinking veloci­ty w (in vertical direction) is essentially

w VJJjr = V/Tw7%s(c^7c^) =

s/(2/gpe)(m/S)'(CD/Cj^ ) (54)

Disregarding any possible influence of Reynolds and Mach numbers, all of the right side of this equation is given for a particular airplane configuration. The sinking velocity is found in part (b) of figure 10.

b	=	131	ft	mean chord = 20 ft
s	=	2433	ft2	horizontal tail = 500 ft2
A	–	7.1	–	angle of sweep = 35 deg
w	=	100	kip	completely empty
w	»	300	kip	with maximum load
к	=	30	deg	і flaps during takeoff
T	*	11000	lb	j continuous rated thrust
at	eea level	for	each of 4 Pratt ft Whitney J-1
Ho	=	3 to 6	107	in flight up to 36,000 ft

Figure 9. Planform view and principle data of the USAF КС-135 tanker airplane (prototype of the Boeing 707 airliner) as of 1958 (21).

Landing. The minimum landing speed of an airplane de­pends on the maximum lift coefficient that can be de­veloped. Since the stopping distance after landing is in­fluenced by the touch down speed, it is desirable to have wing systems that produce as high a CUy as possible. Although drag is important in case of an aborted landing, lower lift drag ratios are acceptable with high values of CLX as high levels of power and lower weights are usually encountered during landing, see Chapter VI.

Thus the landing speed will be some factor, say 1.2 times the stalling speed which is

VL = 1.2 (295W/irSwCu>)//z (55)

Where VL is the landing speed in knots and W the landing weight.

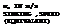
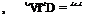
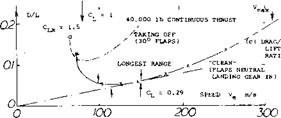Evaluation of KC-135. We are now in a position to derive drag and lift of an airplane and its equivalent velocities (in m/s) either from flight tests or from given drag and lift coefficients. Performance data of the Air Force’s KC-135 tanker (refuelling airplane, prototype of the Boeing 707) are available (26). We are using the flight-tested results, to explain the aerodynamic principles of performance. Di­mensions and data of the airplane (as in 1958) are listed in figure 9. We have assumed W = 200,000 lb, and a com­bined constant thrust of 40,000 lb. Evaluation of the data particularly in (21,a) indicates an extrapolated С^0 = 0.013, and a dC0/dc£ = 0.053. The span efficiency factor is a = 0.84, for “clean” condition (flaps neutral, e landing gear in). The extrapolated minimum drag co­efficient is Cp0 = 0.013, so that approximately

CD =0.013 +0.054 CL[13]

Results are plotted in figure 10, in form of force ratios and equivalent speeds.

Takeoff In case of the KC-135, 30 of flap deflection are recommended for takeoff. A corresponding (D/L) func­tion is shown in part (c) of figure 10. It is seen, however, that after leaving the ground, neutral flaps (and a re­tracted landing gear) provide a much higher rate cf climb.

For Climbing, excess thrust is required. The fastest climb (that is the highest vertical velocity w) is obtained at the speed where (D/L) = minimum, or (L/D) = maximum (as in part (a) of the illustration). We may be fnlcrested, however, in a steep (rather than a fast) climb, say over an obstacle (such as a building). The minimum thrust required to do this for a “clean” airplane corresponds to the minimum of the sinking speed as in part (b) of figure 10. According to equation (55) the optimum speed of lift coefficient is defined by a minimum of the parameter

(C Dicfzy, or (C p /С* );

°r (C 2(f /C(_) (56)

Reasonable numbers are obtained when using (C ^ /CD )• In case of the KC-135, we find at Ve = 100 m/s, a value of 212.

Range. The sailplane mentioned above will travel farthest when gliding along the lowest possible angle, indicated by the tangent from the origin of graph (b). The point found is at the same speed where L/D = maximum, as in part (a) of figure 10. However, in a powered airplane, the miles of distance flown per unit weight of fuel burned, has to be considered. The tangent as in part (c) indicates an opti­mum speed of 150 m/s, for a Cu = 0.29, in the example of the KC-135. Here as in the case of endurance, it has to be taken into account, however, that the weight of the airplane reduces considerably (possibly to half) as the end of the flight is approached (20,g).

Endurance (the number of hours staying aloft with a given supply of fuel) is maximum at the speed where the sinking speed is minimum. This point corresponding again to a minimum of the parameters in equation (56), is found in part (b) of the illustration.

0

IN m/s

EQUIVALENT (INDICATED) AIRPLANE SPEED

ЮО 200 300 400 500^600

SMALLEST GLIDE ANGLE

LONGEST GLIDE LONGEST ENDURANCE AT = 0.66

AND STEEPEST CLIMB

Propeller-Driven Airplanes may have constant engine pow­er available. Even assuming a variable-pitch, constant – speed propeller, neither net power nor thrust are constant, however. Qualitatively, performances are as follows:

a) During the takeoff run, propeller efficiency increases, possibly to near maximum, while thrust reduces.

b) Assuming constant efficiency and constant net power in terms of (T V), maximum climb velocity depends upon excess power (rather than thrust). The corresponding speed V is, therefore, lower than that of a same-size jet-powered airplane.

c) Regarding range, a minimum of (power times time)/(speed times time) = (D V)/V = D has to be found. This will be at the speed where (D/W) = minimum.

d) Both in jet – and in propeller-driven airplanes, maximum altitude (ceiling) and minimum turning circle will approxi­mately be obtained for the point where (C0 /CL ) is mini­mum.