An overall technical assessment

1.2 We begin our survey with a problem that will demonstrate some of the many simplifications and abstractions we usually make and, at the same time, give us some first overall view of the present position and the future prospects. We restrict ourselves to civil transport aircraft. The task is to fly from A to В. We assume that air­fields are provided and are a given quantity. In general, this consists of a whole set of requirements which could be part of the overall design of air­craft. Which A to what В and when and at what speed is determined mainly from economic and social considerations. What the customer – passenger – wants must also be considered. His requirements probably are: safety, com­fort, reliability, and convenient interchanges at intermediate stations, pos­sibly in that order. All this takes a lot of sorting out, and these problems are much debated at present (see e. g. L T Goodmanson & L В Gratzer (1973),

H Wittenberg (1973), C F Bethwaite (1975), C W Clay & A Sigalla (1975), and A H C Greenwood (1975)). It is very important to find good answers since the viability of an aircraft project may depend on them, and since mistakes must be paid for dearly.

For our purpose, we can go back to mechanics and write down the equations of motion of the aircraft. In principle, this can readily be done. Again, we must bear in mind that there are many constraints set by safety regulations, air traffic control, weather, economics, etc. Also, the aircraft must be de­signed in such a way that the solutions of the equations of motion imply that the aircraft is statically and dynamically stable and also controllable so that the human pilot can handle it in all situations safely and without too great a workload.

If the aircraft is regarded as one rigid body, we have six equations of motion which express the conditions that the integral of the products of acceleration times mass element equals the sum of the forces acting on the aircraft; and that the integral of the moments of acceleration multiplied by the mass ele­ments equals the sum of the force moments. The forces include components of the resultant air reactions as well as components of gravity. If we want to take account of the fact that the aircraft has control surfaces, the system is described by many more equations. For example, there are 18, if we in­clude only the main longitudinal controls and still assume that we deal with rigid bodies, simple rigid linkages without friction, and make use of some
properties of symmetry. However, there are conditions when the assumption of rigidity cannot be justified and when the aircraft must be treated as a deform­able body. This brings in structural properties as well as aerodynamic load­ing actions and excitations. The system is then very complex indeed. We can get some idea of the size of the field and of the problems involved from the collection by H R Hopkin (1966) of terms for describing some properties of physical systems. This is a kind of textbook of aircraft dynamics at the same time. Among other textbooks for further reading are those by R von Mises

(1959) and by В Etkin (1959) and (1972). These matters will be taken up again in Section 5.10.

To solve the equations of motion, the integrals are usually expressed in terms of translational and angular velocities and their derivatives. The equations are highly nonlinear in the general case. A large number of simplifications and approximations are usually introduced to make them amenable to treatment. Also, much work is involved in assembling the numerical values for the many derivatives, even if the aircraft and the conditions it flies in are given.

The design problem is the inverse of that: to design aircraft in such a way that the values of the derivatives lead to solutions of the equations of motion, which represent the desired motion according to some given perform­ance, control, and handling criteria. We are not yet able to do that in any generality, but this should be one of the aims for the future: we want an integrated aerodynamic and structural analysis of the dynamics of the flying vehicle as one deformable body, and to use that for design purposes.

We turn now to the specific question of how an aircraft gets from A to В and consider an example where the equations of motion are drastically simplified but still give useful answers. Let the aircraft move with a velocity

ds/dt = v(s, h,t) (1.1)

along a flight path, with s along the flight path, h(s) normal to the ground, and t(s) the time; but let dh/ds *< I. This means that the slope of the flight path is assumed to be small and that its curvature can be ignored. The forces along the flight path are then

where W is the weight of the aircraft, Th is the thrust force along the flight path and D the drag force. If we also know the forces normal to the flight path, i. e. how the weight is supported either by the ground or by aerodynamic lift forces, we have two equations of motion, which can give many useful answers for the whole of the path: rolling along the runway, take-off, climb, cruise, descent, and approach and landing. We do not want to work all this out in detail here, but take an example where we can see the general lines.

If we knew the engine characteristics, i. e. the weight and also the thrust as it depends on the type of engine and on its thermodynamic cycle, its installa­tion, and on the speed and the air density and temperature; if we also knew the drag forces, i. e. the aerodynamic drag as well as the ground rolling resistance, depending on the kind of runway surface; then we could work out a number of things worth knowing, like the length of the ground run, the lift­off speed, the climb angle, etc. These characteristics determine many aspects of the design of aircraft and possibly even the type of aircraft to be used, especially in cases where the ground run is to be short or zero.

If we also knew the airframe self-noise and the noise pattern of the engine, i. e. the machinery noise coming out of the intake and the nozzle as well as the jet noise, we could work out the noise footprint for the particular air­craft along its flight path. Again, this could provide a design criterion: to design aircraft to produce a given noise footprint. This is another job for the future.

We consider here a particular case, namely, the cruise part of the flight path when dh/ds = 0 and the speed is constant: v = V = dR/dt, where we introduce the range R achieved by the aircraft. Then (1.2) simply reads Th ■ D, and the forces normal to the flight path are

L = W – Wp(t) , (1.3)

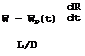where W is the initial all-up weight and Wp(t) is the fuel burnt up to the time t. This is the simplest form the equations of motion can have. But we want to know more: we want to determine the energy which is to be expended for the work to be done per unit time, which is

The energy available from burning the fuel per unit time is

By confining these two equations, we can work out how far the aircraft will fly with a given amount of fuel. For this, we need to know what kind of fuel we have. In (1.5), H is the calorific value of the fuel, i. e. the heat con­tent per unit weight. We assume that there is complete combustion and that the available heat is fully used. It then depends on how this heat is con­verted into thrust work. In (1.5), np measures the thrust work per heat input into the airstream. Finally, it matters how much fuel is burnt per unit time, and this accounts for the term dW /dt.

Г

We have now identified the parameters that dominate this motion. We also introduced figures of merit or efficiencies’. H may be called a chemical efficiency; Пр may be called the propulsive efficiency; L/D, the lift-to-drag ratio, may be called an aerodynamic figure of merit or efficiency: we would like to generate a given amount of lift with as little drag as possible. We can say that np x L/D is a combined aerodynamic propulsive efficiency: it measures the available lift work in terms of the heat input into the airstream. HripL/D is then the available lift work in terms of the heat content in the fuel. All these parameters will turn up again many times in our subsequent discussions.

This can be rearranged to give

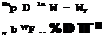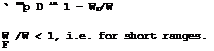where the combinations npL/D and HnpL/D turn up and are assumed to be con­stants. We observe that, at t – 0, no fuel has been burnt and we assume that, at the end of the flight, all the fuel on board, Wp, is used up. Integration over the whole flight time then gives

This is the equation for the socalled Brdguet range. (It is sometimes conven­ient to introduce the specific impulse of the engine, I = Hnp/V, into this equation, or its reciprocal, the specific fuel consumption). The Bre’guet range is an abstract concept and may be regarded as a figure of merit of the whole aircraft. We find, of course, that the design is the better the higher the efficiencies, i. e. it is better in the sense that the aircraft will fly further with a given amount of fuel. Note that, as it happens, the real range does not differ substantially from the Bre’guet range in most cases (see e. g.

D H Peckham & L F Crabtree (1966) and R L Schultz (1974)).

The term (Wp + Wp)/W is in some sense a structural efficiency: the lighter the aircraft can be built, the greater can be the payload Wp and the more fuel it can take for a given all-up weight and so the further it can go. To take this aspect into account, we must consider the weight breakdown of the aircraft. There are several items of a different kind, which make up the overall weight of the aircraft. What interests us, in particular, is the payload so that we can determine in the end how much payload the aircraft can carry over what distances, for a given all-up weight.

As an example, we consider here the weight breakdown for a classical, conven­tional aircraft, following an analysis first used in another context by F Kowalke (1965). As will be explained in detail later, this type of aircraft has separate means for providing stowage space (fuselage), lift (wings), propul­sion (engines), and controls. Thus the weight items can be assigned quite readily as follows: some items must be roughly proportional to the all-up weight: cjW ; these items include the wing, the undercarriage, services and

equipment, and the reserve fuel. Some other items must be roughly propor­tional to the payload: C2Wp ; these items include the payload itself and

also the fuselage weight and the furnishings. Then we have the installed engine weight WE and the fuel weight Wp. Hence, we have altogether

In this relation,	W = cpW + C2Wp + Wg +	Wp .		(1.9)
	W /W = 1 – e-R/HV/D * Г	R		(1.10)
	Hn L/D P
from (1.7) and (1.8). WP 1 (	The payload fraction is then "e. V) , J_ /, . c C1 w W/ c2 ^ 1	WE	R і ^
-2- = —1 1 – W c2	W	Hn L/D 1 P ‘	• (1.11)

To obtain an overall view, we want some actual numbers to relate the payload to the range, for various given efficiencies and weight factors.

We begin with fuels and their chemical efficiencies. At present, kerosene is generally used and the numbers given below are typical values for room

. . , 3. ,	kerosene -O	hydrogen	hydrogen kerosene
Specific volume [m /kg]	0.124 x	10	1.42 x 10 z	11.3
Specific weight [N/m ]	7.9 x	103	0.69 x 103	0.088
Calorific value [m]	4.35 x	106	11.75 x 106	2.7
Air required for stoichiometric mixture	14.8		34.2	2.3
[kg(air)/kg(fuel)] Heat content [J/kg(air)l	2.88 x	106	3.38 x 106	1.2

temperature. In future, other fuels with a higher energy content may be used, such as liquid methane or hydrogen (fdr a discussion of energy resources see e. g. P Kent (1974) and Anon (1974)). Therefore, some typical values for liquid hydrogen are also given in the table (see e. g. R W Haywood (1972)), We note, ,

the high calorific value of hydrogen, which is 2.7 times that of kerosene, but also the relatively high specific volume and its correspondingly low specific weight. The weight of air required for stoichiometric combustion is also relatively high, but the heat content in terms of the mass of air required for combustion is much the same for both fuels. The calorific value is given in metres when the heat content, is expressed by its mechanical equivalent. To make up for mechanical and thermal energy losses, in general practice, air­craft carry more fuel than the payload, depending on how far they want to go.

On this count alone, Wp must go down as R increases. We shall see later in Chapter 8 that possible future types of aircraft, which fly fast over very long ranges, may allow hydrogen fuel to be used. That will compensate in part for the reduction of the payload with range.

For a general assessment, we may take the product npL/D together. As we shall see in Chapter 3, the basic physics are such that both factors are pri­marily functions of the Mach number M, if we think in terms of a series of types of engine and a series of types of aircraft:

Пр – f(M) ; L/D – g(M)

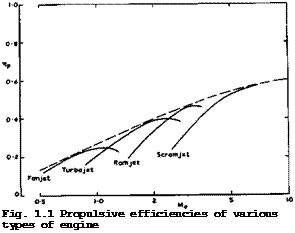The propulsive efficiencies may be interpreted as values from an envelope to the individual efficiencies of a whole series of different types of jet engine, as indicated schematically in Fig. 1.1. The engines, from the fanjet to

LIVE GRAPH

Click here to view

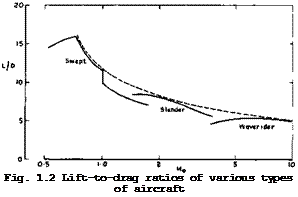the supersonic-combustion ramjet, will be the basis of further discussions below. Likewise, the lift-to-drag ratios belong to an envelope pertaining to a whole series of types of aircraft, as indicated schematically in Fig. 1.2. These are the three major types of aircraft, – classical and swept-winged

aircraft, slender aircraft, and waverider aircraft – , which are the main

subjects of this book. Only some of these values have been realised in prac­tice. At present, we are labouring somewhere between M – 0.7 and M = 0.9 at high-subsonic speeds. Then we have the Concorde and the TU 144 at M = 2. The other engines and aircraft are hypothetical and still to come.

For our first assessment we assume that, very roughly, f(M) increases and g(M) decreases with M such that

TlpL/D ■ – constant (1.12)

Present technology may be described roughly by Kap – n, but the value of Kap is certain to increase as we progress. KaP * 5 may be regarded as representing hypothetical improvements which are not very optimistic. To fix some numbers in our minds, Kgp ** ir may be thought of as implying the following individual values:

M	= 0.7	1.2	2	10
Пр	= 0.2	0.3	0.4	0.6
L/D	– 16	10	8	5

To fix some ideas in our minds, these numbers mean that we do not have to pay for speed, to a first order. The range factor R/(HTipL/D) in (1.10) and (1.11) does not depend on the flight speed but only on the range itself. Thus the fuel fraction according to (1.10) is directly proportional to the range and does not depend on speed. Very roughly – about half the weight of an aircraft at the beginning of a flight across the Atlantic is that of fuel, irrespective of whether it takes a long time about it and flies at a subsonic speed or whether it does it more quickly and flies at a supersonic speed. This is a remarkable property, quite unlike what is found for other means of trans­port. We shall substantiate and qualify this in more detail in later chapters but we can note here already that this is not only a consequence of (1.12), according to which the propulsive efficiency may be expected to improve with speed at much the same rate as the aerodynamic figure of merit L/D may fall. It is also a consequence of our ability to generate thrust in jet engines by relying more and more on direct heat addition to the airstream, as the speed
increases, rather than on supply of mechanical energy. Thus the thrust of a given engine tends to be roughly independent of the speed, whereas a piston engine, for example, will tend to deliver a constant horsepower so that the thrust tends to fall with speed. Further, jet engines can operate at higher altitudes so that the actual drag of the aircraft, which is roughly propor­tional to Po^o^» can be kept down by flying higher. We note that aircraft with propellers driven by piston engines could not do this, nor could air­ships. No other known means of transport has the potential capability to in­crease the speed when the distance to be covered becomes longer and hence to keep the travelling time about constant. All this follows from the physics involved: they favour flight.

For the structural factors in (1.11), c^ = 0.35 and C2 = 2.5 are rather conservative values on present technology. Again, improvements should be pos­sible and we should be able to achieve c^ = 0.25 and C2 = 2.0 in a decade

or two. The engine weight fraction W^/W is about 0.1 for the classical type of aircraft with turbojet propulsion. We take that value for the present assessment although engines for supersonic flight may be somewhat heavier, as will be engines for shorter than conventional take-off and landing. Further, we make some allowance for the difference between the real range and the

Brgguet range and also for the extra fuel reserve which has to be carried for

possible diversions and for holding flights. Thus we put R-100 instead of R (measured in km) .

We may look at the technical prospect before us first in economic terms and assess the ooet8 involved in transporting people and goods by air. Roughly, the operating costs are related to the hours flown and to the payload the air­craft can carry. The revenue is related to the kilometres covered. Both are related to the seat-kilometres obtained in a given time. The parameters that interest us in economic terms are, therefore, Wp/W, R/R, and the product (Wp/W)(R/Rg) as a measure of the seat-kilometres produced in relation to the cost of building and moving the aircraft. We have introduced here as a stan­dard length the value Rg = 2 x 104 km, which is half the earth’s circumfer­ence and hence the ultimate global range. We also want to take the flying time into account. For the present assessment, we may use the Breguet time

T = 8.4 R 10-4 / M, (1.13)

where the time is measured in hours, the range in kilometres, and where the velocity of sound has been put equal to 330 m/s.

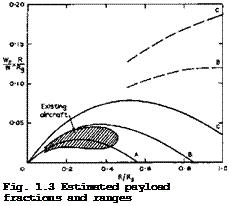
Estimates for past, present, and potential future payloads and seat-kilometres are shown in Fig.1.3. As explained above, the values for the three curves labelled А, В, C are as follows:

	C1	c2	npL/D
A	0.35	2.50	3
В	0.30	2.25	4
C	0.25	2.00	5

The full lines in Fig.1.3 are for kerosene fuel, and the dashed lines indicate what could be achieved with the same technology as for curves В and C if hydrogen could be used as fuel. Fig. 1.3 also gives a very rough indication of the main speed ranges of application for the three major types of aircraft. The shaded area gives some indication of where we are now and of the region inhabited by existing aircraft. How small it is compared with what is still to come! The first generation of turbojet aircraft, designed in the 1950s,
lie on the lower boundary of the shaded region. The upper boundary approxi­mates current aircraft. It is a remarkable but little-known achievement that, within a short period of 15 to 20 years, the technical and economic figures of merit have been improved by about 50% for short-range aircraft and have been about doubled for medium-range aircraft. It is also remarkable that the improvements that may confidently be expected in aircraft may be even bigger. Future developments should include not only new types of aircraft with in­creased speeds and ranges but also quite substantial progress in the design of existing types of aircraft. They can be made much more economical, quite

LIVE GRAPH

Click here to view

apart from improvements in safety, comfort, reliability, and environmental acceptability to the public. Concorde is a typical case: as a first-

generation aircraft, it lies on the lower boundary of the shaded region; but it must be seen as the first of a line of successively improved members of a family of aircraft. There is no physical reason why its economic value could not also be doubled in the course of its evolution.

Fig.1.3 does not present the whole story since distances are measured as a length in km. As we shall see in Section 1.3, distances, in human rather than economic terms, should be measured by the time taken to cover them. Then we find that some of the aircraft in the presently inhabited area take a very long time to get to their destination. For example, to fly across the Atlan­tic at M – 0.7 takes about 7 hours Bre’guet time, on present technology. This could be shortened to about 5 hours if the technology could be improved to fly at M ■ 0.95 and to about 4 hours if we could reach M – 1.2. But a

reasonable time of about two hours can only be achieved by flying supersonic­ally at about M = 2. This is the job for Concorde and its successors.

A scale has been added to Fig. 1.3, which gives the value of the Mach number needed to achieve about two hours flying time. It links design range with speed: the further, the faster. This means that aircraft with a range longer than that of Concorde should fly at high-supersonic or hypersonic speeds. It is then that we can seriously consider the use of high-energy fuels, as we shall discuss in detail in Chapter 8. To achieve a global range (R/Rg – 1), we should design aircraft to fly at Mach numbers up to around 10.

At this point, we may conclude that the technical prospects for future deve­lopments in aviation are very bright and far-reaching. We note that we have argued the technical case on the basis of known physical principles and fun­damental concepts in fluid mechanics. We are thinking of further exploration and exploitation of these principles. Thus we can only conclude that the main growth of aviation is still to come and that the much-maligned liberal belief in progress is not just an unrealistic dream but a realistic aim. "To deride the hope of progress is the ultimate fatuity, the last word in poverty of spirit and meanness of mind" (F В Medawar (1972); see also D Ktlchemann

(1970) and I I Glass (1974)).