Apparent mass

It is useful to note that the dimensional lift/span corresponding to ciA given by (7.56) is

L’a = pU2cctA = m’A(h + U0) (7.57)

mA = pn(c/2)2 (7.58)

where mA is the apparent mass (per unit span), which is the mass of a unit-span cylinder of fluid whose diameter is airfoil chord. Hence, subjecting an airfoil to a normal acceleration results in an additional reaction force as though this cylindrical mass of the air was attached to the airfoil and also accelerated. The effective normal acceleration, in addition to h, also includes a Coriolis-like term Uв due to airfoil rotation.

3.1.7 Sinusoidal motion solution

Theodorsen [56] derived solutions for the case of small-magnitude sinusoidal motion at some frequency w, specifically for use in predicting wing flutter. This situation is most conveniently treated by the introduction
of complex variables,

h(t)	= ho cos (ut + ф^	= Re{h elwt} ;	h = ho e1^	(7.59)
0(t)	= 0o cos (ut + фв)	= Re{0elwt} ;	9 = 0o e1^	(7.60)

where the convenient complex amplitudes h, 9 incorporate both the heave and pitch amplitudes ho,9o, and also the heave and pitch phase angles ph,^e. The notation Re{} denotes the real part of a complex quantity.

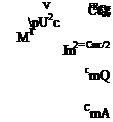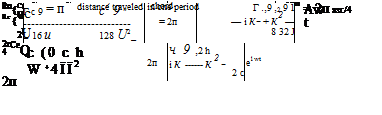Substitution of the sinusoidal h(t) and 9(t) expressions above into the general-motion Wagner solutions (7.55) and (7.56), gives the following solution for the lift coefficient, again as a sum of quasi-steady and apparent – mass contributions. The pitching moment coefficient can also be obtained.

The dimensionless parameter k which appears in this Theodorsen solution is the reduced frequency, which was previously mentioned in Section 1.5.3. It affects the strength of the shed vorticity, and also is a measure of the relative importance of the ф term in the unsteady Bernoulli equation (7.19). The other relevant parameters which appear are the maximum heave/chord ratio ho/c, the maximum pitch displacement 9o, and the relative phase фh — фв between the heave and pitch motions.

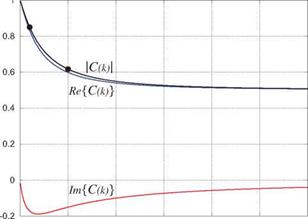
For finite values of k, the circulatory parts of the lift and moment in (7.61) and (7.64) are modified by the Theodorsen Lag Function C(k) factor. This is a complex quantity, and is explicitly defined in terms of standard and modified Bessel functions J0, J1 and Y0,Y, respectively.

Ho(k) = Jo(k) — i Y0(k) , Hi(k) = Ji(k) — i Yi(k)

Hi(k) + iHo(k)

Its real and imaginary components and its magnitude and phase angle are plotted in Figure 7.10.

In the quasi-steady limit k ^ 0 the lag function becomes unity, C(o) = 1 + 0i, and also all the time-rate terms in the unsteady lift and moment expressions become negligible. The resulting lift and moment coefficients then reduce to cg = 2па, cmc/2 = cg/4, which matches thin airfoil theory.

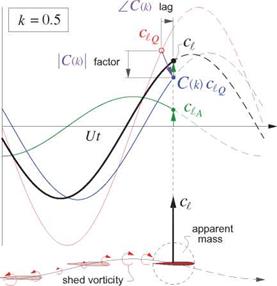
For k>0 we have |C(k)| < 1 and ZC(k) < 0, so the lift contribution of cgQ will now be reduced in magnitude and will also have a phase lag. The main origin of these effects is the convection of shed vorticity into the wake. This contributes a vertical velocity w at the airfoil which tends to oppose the current angle of attack,
and thus reduces the lift magnitude. But this vertical velocity contribution is delayed by the vorticity’s convection time into the wake, which results in the phase lag.

As in the general-motion result (7.56), the remaining aA and cmA “apparent-mass” parts act instantaneously. Because of their extra time derivatives these introduce phase leads into the lift and moment, but become significant only at larger k values. Figure 7.11 shows the relative magnitudes of these various contributions to the lift for sinusoidally-heaving airfoils at two different reduced frequencies.

0 0.5 1

1.5 k 2 2.5 3

3

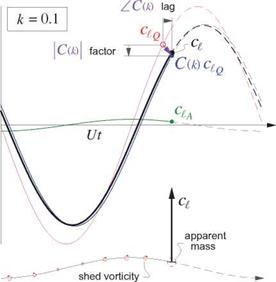Figure 7.10: Real and imaginary parts, and magnitude and phase of the Theodorsen lag function. Magnitude and phase lag values at k = 0.1 and k = 0.5 are used in the example in Figure 7.11.

Figure 7.11: Unsteady lift coefficient components of airfoils undergoing sinusoidal heaving at zero pitch angle. Only the physical (real) parts are shown. The two airfoils have the same heave amplitude and wavelength, but different chords and hence different reduced frequencies k = n x chord/wavelength. The quasi-steady lift ciQ = 2па3с/4 is lagged and reduced in magnitude by the C(k) Theodorsen function associated with shed vorticity. The impulsive lift contribution Qa is the inertial reaction of the fluid’s apparent mass subjected to vertical acceleration, and leads the quasi-steady lift by 90o.