Bu1bbly liquids

In the previous sections we used the analogy of Lighthill (1952-54) to obtain a scaling law for sound production by subsonic isothermal free jets. One of the choices in this derivation is to express the analogy in terms of fluctuations of density p’ (equation 40). As an alternative, we could have also used the fluctuations of pressure p’ (equation 39). In principle both formulations are equivalent as long as no approximations are involved. However, an analogy is only meaningful if we do use approximations. De­pending on the choice of the aero-acoustic variable some approximations will appear naturally. For example using the pressure formulation, the en­tropy noise source term has the form d2(p’/c2 — p’)/dt2. This is a monopole sound source, to be understood as the time dependent volume expansion due to unsteady combustion. A more detailed analysis of thermal effects is provided by Morfey et al. (1978) and Dowling [in, Crighton et al. (1992)]). Using the density formulation, the entropy sound source term is a spatial derivative d2 (p’ — c2p’)/dx2. We will now explain the physical meaning of this apparently obscure sound source term. For this we consider the sound

produced by a turbulent free jet in a bubbly liquid, as observed by a lis­tener immerged in the pure liquid. In such a case the speed of sound c in the source region is much lower than the speed of sound c0 of the fluid surrounding the listener.

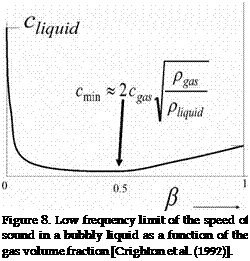
Considering the low frequency limit of the behaviour of a mixture of gas bubbles and a liquid (Figure 8). We find that low frequency implies that gas density pg and fluid density pi are both uniform so that the mixture density p is given by [Crighton et al. (1992)]:

P = вРд + (1 – в)Р1 (133)

where в is the volume fraction of gas in the mixture. Assuming a quasi­steady behaviour, the pressure is uniform. Thus, we can add the compress­ibility of the two phases to obtain the compressibility of the mixture:

JL = _A_ і (1 – в)

pc2 Pg c2 Plcl

where cg is the speed of sound in gas and ci is the speed of sound in liquid.

Eliminating the density by multiplying (133) by (134) yields:

For air/water mixtures at neither too small or too large a value of в we can neglect both the contribution of air to the mass density and the contribution of water to the compressibility. We then get:

For air with (pg = 1.2kg/m, cg = 340m/s) and water with (pi = 1000kg/m, ci = 1500m/s) we get a minimal speed of sound cmin « 20m/s at в = 0.5 . The entropy term in the analogy of Lighthill for an isentropic flow can be written as follows:

d 2 d 2 / c2

■Щ p — c0P’> = щp (l – ^ . (137)

The pressure fluctuations in the source region are of the same order as the fluctuations in the Reynolds stress tensor: p ~ pU2. Hence, compared to a free jet of water surrounded by water, the bubbly liquid turbulence sound is enhanced by a factor |(1 — c2/c2)| = 5 x 103, which is 74 dB. Infact, taking a shower in a bath tub, we observe that the water jet impinging on the water surface is much noisier than the jet immerged in the water, as we can understand qualitatively in terms of the analogy of Lighthill. According to Morfey (1973) and Powell (1990) this entropy term can be understood as the sound produced by the unsteady force exerted on the mixture as a result of the “buoyancy” force due to the difference in density between the two phases undergoing a pressure gradient. This corresponds to a slip between the two phases. Obviously, as there are no net external forces, this sound source must be a quadrupole, the force of the gas on the liquid being balanced by the reaction force of the liquid on the gas.

Similar effects, though much weaker can be found in non-isothermal gas free jets. Contrary to earlier literature predicting a dipole [Morfey (1973), Obermeier (1975)], recent studies indicate that the overall acoustic power level radiated by hot jets is also in line with the height power law of Lighthill [Viswanathan (2009)], which actually confirms that this sound source is also a quadrupole. In the early literature it was also suggested that next to con­vection effects due to density differences, the heat transfer between a hot
gas free jet and its surroundings would generate a monpole sound source. In cases with ideal gasses and a uniform constant Poisson ratio y, this does not occur due to the jet contraction by cooling compensating exactly expansion of the surroundings due to heating [Morfey and Wright (2007)]. Monopole sound sources do occur as a result of combustion or phase transition (mois­ture condensation).

Bubble resonance can induce an even larger amplification of turbulent sound production [Dowling and Ffowcs Williams (1983)]. Yet, it is argued by Crighton (1975) that typical turbulent eddies corresponding to frequencies close to resonance frequencies of bubbles are much smaller than the bubbles and can therefore not excite the bubbles coherently. He therefore uses the low frequency approximation described above.