Error Indication Based on the Adjoint Solution

This section describes the use of the adjoint information as a sensor for the error indication in the TAU adaptation. The main work was the development and imple­mentation of the adjoint solver which is described in the contribution Adjoint-Based Error Estimation and Functional Correction of this volume. The adjoint solver provides a field variable containing a kind of measure for the local discretization error weighted with its influence on the target functional, which may be the integral lift or drag coefficent. This variable serves as an interface to the grid adaptation tool.

The work at the adaptation tool itself which was needed to enable an adjoint – based adaptation was more of technical nature. Because the provided adjoint in­formation has to be regarded as a pointwise error indicator and the adaptation tool works edge orientated, the sum of the sensor variables for the edge points has to be used as the edge indicator. Similar to the differences-based indicators, a weighted

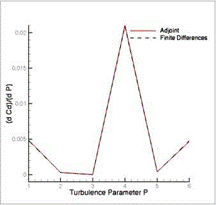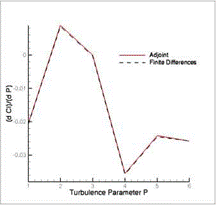
Fig. 17 Sensitivity of lift (left) and drag (right) coefficients w. r.t. variations in the model parameters P of the SAE turbulence model, calculated by adjoint method

Fig. 18 Sensitivity of lift (left) and drag (right) coefficients w. r.t. variations in the model parameters P of the Wilcox-k-m turbulence model, calculated by adjoint method combination of different variables of the adjoint sensor file can be used for error indication in the TAU adaptation.

The adjoint-based adaptation was tested in a simulation for the HIRENASD – model. The initial grid was generated with the Solar grid generator [8]. It has 3.12 million points and consists of 2.54 million hexhedra, 20758 prisms, 40430 pyramids and 3.19 million tetrahedra. The flow was calculated for a Mach number of Ma = 0.8, an angle of attack of a = 1.0° using the Spalart-Allmaras turbulence model in its original version.

After the solution was well converged, the adjoint problem was calculated for the integral drag coefficient as the target funtional. Using the adjoint sensors on the one side and the differences of gradients for comparison on the other side, the grid was

Table 6 Results of simulations using the differences-based and the adjoint-based adaptation initial grid adapt +50% adapt +100% global +353% differences- Cl 2.783e-1 2.787e-1 2.786e-1 2.789e-1 based Cd 1.181e-2 1.188e-2 1.186e-2 1.171e-2 adjoint-based Cl 2.783e-1 2.773e-1 2.774e-1 2.789e-1 target: CD Cd 1.181e-2 1.175e-2 1.170e-2 1.171e-2

adapted with 50% and 100% new points. Table 6 shows the results of the integral lift and drag coefficents. These results are compared to the results for the initial grid and the globally refined grid. As already discussed in Section 2 and Subsection 3.2, the result on the globally refined grid serves as reference value in case of a locally adapted calculation.

The differences-based adaptation leads to improved results for the lift coefficient, but not for the drag coefficient. It seems that the differences are not appropriate for estimating the local discretization error in this example. Contrary, the adjoint-based adaptation improves the results for the drag coefficient significantly. Because the drag coefficient was used as target functional for the adjoint-based adaptation, an improvement of the lift coefficient result is not expected in this case.

The process was restarted for the example with 50% new points. The results are documented in Table 7 and the resulting grids of the adjoint-based case are shown in Fig. 19. The adaptation used re – and de-refinement and the twice adapted grid has some de-refined grid areas.

The adjoint-based adaptation is significantly more expensive in terms of compu­tational effort. The differences-based adaptation usually can already be performed for a not fully converged solution, especially in case of a computation with mul­tiple adaptations. The resulting grid will not differ very much from that generated by adaptation for the fully converged solution. Different from that, an adjoint cal­culation requires a very well converged solution. Additionally, the adjoint solution needs computational resources comparable to the original solver and nearly an order of magnitude more memory.

The application of the adjoint-based adaptation requires a careful choice of the control parameters to get the best effect from the much better, but expensive error

Table 7 Results of a twice adapted simulation using the differences-based and the adjoint – based adaptation initial grid adapted +50% 2x adapted +50% differences- Cl 2.783e-1 2.787e-1 2.790e-1 based Cd 1.181e-2 1.188e-2 1.190e-2 adjoint-based Cl 2.783e-1 2.773e-1 2.780e-1 target: CD Cd 1.181e-2 1.175e-2 1.177e-2

Fig. 19 Grids resulting from adjoint-based adaptation: initial grid (top left), once adapted grid (top right), twice adapted grid (bottom)

estimation. For example, if the percentage of new points is chosen too small, the differences-based adaptation might achieve the same result, using much more points with a similar computational effort. On the other hand, the point number and the resulting grid should not get near the global refinement. In this case the influence of a better refinement indicator would be smaller.

Thus, further systematical tests are needed to find a best practice strategy for the adjoint-based adaptation.