Euler’s Equation of Motion

The principle of conservation of mass, applied to an elemental control surface, led to Equation 2.17, which must be satisfied everywhere in the flow. Similarly, the momentum theorem applied to the same element leads to another set of equations that must hold everywhere.

Referring again to Figure 2.7, if p is the static pressure at the center of the element then, on the center of the right face, the static pressure will be

| dp Ax + dx 2

This pressure and a similar pressure on the left face produce a net force in the x direction equal to

dp *„

Since there are no body forces present and the fluid is assumed inviscid, the above force must equal the net momentum flux out plus the instantaneous change of fluid momentum contained within the element.

The momentum flux out of the right face in the x direction will be

Out of the upper face the corresponding momentum flux will be

Similar expressions can be written for the momentum flux in through the left and bottom faces.

The instantaneous change of the fluid momentum contained within the element in the x direction is simply %

~(pu Ax Ay)

Thus, equating the net forces in the x direction to the change in momentum and momentum flux and using Equation 2.17 leads to

du 8u du _ 1 dp

dt U dx V dy p dx

Generalizing this to three dimensions results in a set of equations known as Euler’s equations of motion.

du , dU, dU, dU 1 dp

dv, dv , dv, dv 1 dp

—+И— +U— + w — =—— r~

dt dx dy dz p dy

dw, dw, dw, dw 1 dp

——+ U — + V ——+ w——=———————— r-

dt dx dy dz p dz

Notice that if и is written as u{x, y, z, t), the left side of Equation 2.22 is the total derivative of u. The operator, d( )ldt, is the local acceleration and exists only if the flow is unsteady.

In vector notation Euler’s equation can be written

§ + (V – V)V = –Vp (2.23)

ol p

If the vector product of the operator V is taken with each term in Equation 2.23, Equation 2.24 results.

<0 is the curl of the velocity vector, V x V, and is known as the vorticity.

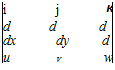(2-25)

One can conclude from Equation 2.24 that, for an inviscid fluid, the vorticity is constant along a streamline. Since, far removed from a body, the flow is usually taken to be uniform, the vorticity at that location is zero; hence, it is zero everywhere.