EXAMPLE

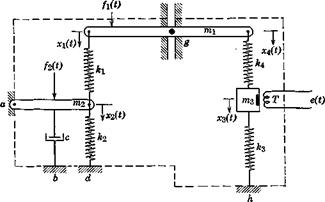
Figure 3.1 shows a system S comprising a planar arrangement of rigid bodies mit massless springs Jct, viscous damper c, and an inductive displace­ment transducer T. (Its voltage is e(t) = const. x3.) The midpoint g of т1г and mass m3, are constrained to move vertically. The system, bounded by the dashed line, is made up of all these separate elements. The nonautonomous

inputs are the arbitrary external forces and /2 acting on the masses and the state variables are the coordinates of the joints, xft), their velocities vft) = xit and the voltage e{t) of the transducer. Any of this set might be taken as outputs. Here, however, the output happens to be e(t). If fx and/2 were zero, the system would be autonomous and capable only of free vibration associated with nonequilibrium initial conditions. The external reactions at the points of connection to the fixed base, a, b, d, h, and g are functions of the state variables xi and vit and hence are autonomous inputs. The parameters of the system are the masses of mt, the stiffnesses of Jcit the damping constant of c, the transducer constant, and the geometrical di­mensions. It should be pointed out that although there is a minimum number of coordinates (state variables xt and vf) required to specify the state of the system, eight in this example, this number may be arbitrarily increased by redundant variables if it is convenient to do so. For example, we might add the transducer output, the four accelerations a( = vf, and the forces in the springs, even though they are, by virtue of the physical laws governing the system, not independent of the x( and vt. (Indeed the mathematical statement of this dependence is the main ingredient in the formulation of the system equations.) The minimum number of state variables required is the order of the system.

The arbitrariness of the choice of system, and its dependence on the aim of the investigation is illustrated by the fact that we might choose as a system for study any of the individual elements of S, or any of the subsystems obtained by combinations of them. Furthermore, the set of state variables might be still further augmented by adding sudh items as the stresses and strains in m1 and m2.

Finally, the release of simplifying approximations such as rigidity of the bodies, and masslessness of the springs, would require further elaborate additions to the state variables.