FLOW WITH HIGH REYNOLDS NUMBER

The most important outcome of the nondimensionalizing process of the governing equations is that now the relative magnitude of the terms appearing in the equations can be determined and compared. If desired, small terms can be neglected, resulting in simplified equations that are easier to solve but still contain the dominant physical effects.

In the case of the continuity equation all terms have the same magnitude and none is to be neglected. For the momentum equation the relative magnitude of the terms can be obtained by substituting Eqs. (1.51-1.56) into Eq. (1.50), and for the x direction we get

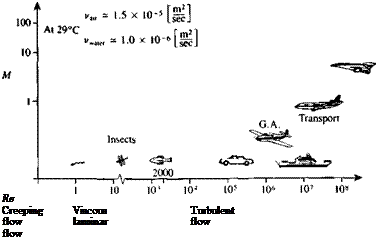Before proceeding further, let us examine the range of Reynolds number and Mach number for some typical engineering problems. Since the viscosity of typical fluids such as air and water is very small, a large variety of practical engineering problems (aircraft low-speed aerodynamics, hydrodynamics of naval vessels, etc.) fall within the Re »1 range, as shown in Fig. 1.13. So for situations when the Reynolds number is high, the viscous terms become small compared to the other terms of order 1 in Eq. (1.60). But before neglecting

FIGURE 1.13

Range of Reynolds number and Mach number for some typical fluid flows.

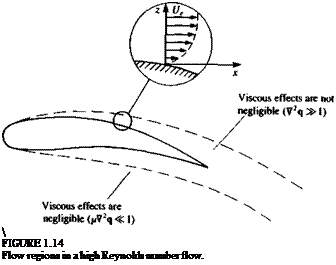these terms, a closer look at the high Reynolds number flow condition is needed. As an example, consider the flow over an airfoil, as shown in Fig. 1.14. In general, based on the assumption of high Reynolds number the viscous terms of Eq. (1.60) (or 1.30) can be neglected in the outer flow regions (outside the immediate vicinity of a solid surface where V2q== order 1). Therefore, in this outer flow region, the solution can be approximated by solving the incompressible continuity and the Euler equations:

V • q = 0 (1.61)

da Vd

^ + q-Vq = f(1.62)

Equation (1.62) is a first-order partial differential equation that requires a boundary condition on one velocity component on a solid surface compared to a boundary condition on the velocity vector needed for Eq. (1.30) in the previous section. Since the flow is assumed to be inviscid, there is no physical reason for the tangential velocity component to be zero on a stationary solid surface and therefore what remains from the no-slip boundary condition (Eq. (1.28a, b) is that the normal component of velocity must be zero

qn = 0 (on solid surface) (1.63)

However, a closer investigation of such flow fields reveals that near the solid boundaries in the fluid, shear flow derivatives such as V2q become large and the viscous terms cannot be neglected even for high values of the Reynolds number (Fig. 1.14). As an example, near the surface of a streamlined two-dimensional body submerged in a steady flow in the x direction (with no body forces) the Navier-Stokes equations can be reduced to the classical
boundary-layer equations (see Schlichting,16 p. 131) where now x represents distance along the body surface and z is measured normal to the surface. The momentum equation in the x direction is

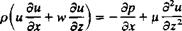(1.64)

and in the normal, z direction:

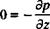(1.65)

So, in conclusion, for high Reynolds number flows there are two dominant regions in the flowfleld:

1. The outer flow (away from the solid boundaries) where the viscous effects are negligible. A solution for the in viscid flow in this region provides information about the pressure distribution and the related forces.

2. The thin boundary layer (near the solid boundaries) where the viscous effects cannot be neglected. Solution of the boundary-layer equations will provide information about the shear stress distribution and the related (friction) forces.

For the solution of the boundary-layer equations, the no-slip boundary condition is applied on the solid boundary. The tangential velocity profile inside the boundary layer is shown in Fig. 1.14 and it is seen that as the outer region is approached, the tangential velocity component becomes independent of z. The interface between the boundary-layer region and the outer flow region is not precisely defined and occurs at a distance <5, the boundary-layer thickness, from the wall. For large values of the Reynolds number the ratio of the boundary-layer thickness to a characteristic length of the body (an airfoil’s chord, for example) is proportional to Re m (see Schlichting,16 p. 129). Therefore, the normal extent of the boundary-layer region is negligible when viewed on the length scale of the outer region.

A detailed solution for the complete flowfleld of such a high Reynolds number flow proceeds as follows:

1. A solution is found for the inviscid flow past the body. For this solution the boundary condition of zero velocity normal to the solid surface is applied at the surface of the body (which is indistinguishable from the edge of the boundary layer on the scale of the chord). The tangential velocity component on the body surface Ue is then obtained as part of the inviscid solution and the pressure distribution along the solid surface is then determined.

2. Note that in the boundary-layer equations (Eqs. (1.64) and (1.65)) the pressure does not vary across the boundary layer and is said to be
impressed on the boundary layer. Therefore, the surface pressure distribu­tion is taken from the inviscid solution in (1) and inserted into Eq. (1.64). Also, Ue is taken from the inviscid solution as the tangential component of the velocity at the edge of the boundary layer and is used as a boundary condition in the solution of the boundary-layer equations.

The solution for a high Reynolds number flow field with the assumption of an inviscid fluid is therefore the first step towards the solution of the complete physical problem. (Additional iterations between the inviscid outer flow and the boundary-layer region in search for an improved solution are possible and are discussed in Chapters 9 and 14.)