FORCES IN A FLUID

Prior to discussing the dynamics of fluid motion, the types of forces that act on a fluid element should be identified. Here, forces such as body forces per unit mass f, and surface forces that are a result of the stress vector t will be considered. The body forces are independent of any contact with the fluid, as in the case of gravitational or magnetic forces, and their magnitude is proportional to the local mass.

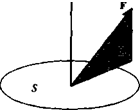
To define the stress vector t at a point, consider the force F acting on a planar area 5 (shown in Fig. 1.4) with n being an outward normal to S. Then

‘"Sid)

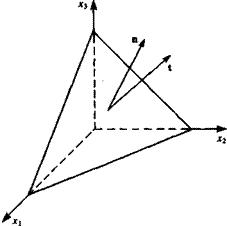
In order to obtain the components of the stress vector, consider the force equilibrium on an infinitesimal tetrahedral fluid element, shown in Fig. 1.5. According to Batchelor11 (p. 10) this equilibrium yields the components in the JC], x2, and x3 directions,

= X топ/ і = 1. 2, 3 (1.7)

/=і

where the subscripts 1, 2 and 3 denote the three coordinate directions. A similar treatment of the moment equilibrium results in the symmetry of the stress vector components so that т/; = r;i.

These stress components xtj are shown schematically on a cubical element in Fig. 1.6. Note that r,, acts in the xt direction on a surface whose outward normal points in the x, direction. This indicial notation allows a simpler presentation of the equations and the subscripts 1, 2, and 3 denote the coordinate directions x, y, and z, respectively. For example,

Xi=X x 2 = y x3 = z

Яг = и Я2 = У q3=w

The stress components shown on the cubical fluid element of Fig. 1.6. can be

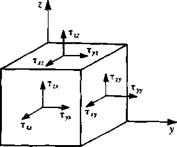
FIGURE 1.6

Stress components on a cubical fluid element.

= *,,

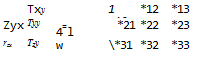summarized in a matrix form or in an indicial form as follows:

Also, it is customary to sum over any index that is repeated, such that

з

2 *</«, = Tijfij for і = 1,2,3 (1.9)

i=i

and to interpret an equation with a free index (as і in Eq. (1.9)) as being valid for all values of that index.

For a Newtonian fluid (where the stress components r,7 are linear in the derivatives dqj dxj), the stress components are related to the velocity field by (see, for example, Batchelor,11 p. 147)

i=j i*j

where ju is the viscosity coefficient, p is the pressure, the dummy variable к is summed from 1 to 3, and dq is the Kronecker delta function defined by

When the fluid is at rest, the tangential stresses vanish and the normal stress component becomes simply the pressure. Thus the stress components become

-p	0	°
0	-P	°	(1.11)
0	0	-PI

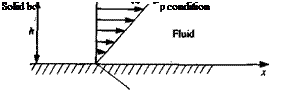
Another interesting case of Eq. (1.10) is the one-degree-of-freedom shear flow between a stationary and a moving infinite plate with a speed 14, (shown in Fig. 1.7), without pressure gradients. This flow is called Couette flow (see,

for example, Yuan,12 p. 260) and the shear stress becomes

Эи ції a,

x” = flTz = – T

Since there is no pressure gradient in the flow, the fluid motion in the x direction is entirely due to the action of the viscous forces. The force F on the plate can be found by integrating txz on the moving upper surface.