Joukowski Airfoil at Incidence

The same result for the potential function is obtained in this case with e > 0 and

8 > 0

, Г

Ф = 2Ua’ cos(0 – a) – (в – a) (2.106)

2n

where now a’2 = (a + e)2 + 82, with the following formula for the circulation that enforces the Kutta-Joukowski condition

Г = 4n U ((a + e) sin a + 8 cos a) (2.107)

and lift coefficient

Cl = 2n 1 +—sin a + cos a (2.108)

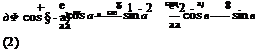The exact solution is quite complicated and is best calculated numerically. How­ever, assuming small values for thickness and camber, i. e. | ^ 1 and 8 ^ 1, the formula can be linearized to give the x-component of velocity as

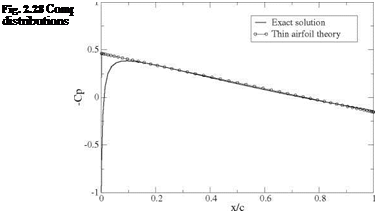
This formula holds for all values of incidence, |a|< 2. For small values of a the small disturbance result is recovered. For example, for a = 8 = 0 and i = 0.077 corresponding to a 10 % thick symmetric Joukowski airfoil, the pressure coefficient at zero incidence is shown in Fig.2.28.

The thin airfoil solution is a straight line, since the perturbation velocity in x’ is linear

U+^’) = U(1 + 57! C (3 – 4 f))

To find the solution in the physical plane and in particular the surface velocity for arbitrary Joukowski airfoils, the values of the potential function at certain points on the circle, image of the profile, are first calculated. The same values are assigned to the corresponding points on the airfoil which can be found from the transformation formulae. The surface velocity can be evaluated numerically as

АФ

V = (2.112)

As

where АФ is the difference between the values of Ф at the two close points on the surface and As is the length of the airfoil segment between these two points. The surface pressure distribution is readily obtained from Bernoulli’s law, i. e.

(2.113)