LIFT AND PITCHING MOMENT OF THE TAIL

The forces on an isolated tail are represented just like those on an isolated wing. When the tail is mounted on an airplane, however, important interferences occur. The most significant of these, and one that is usually predictable by aerodynamic theory, is a downward deflection of the flow at the tail caused by the wing. This is character­ized by the mean downwash angle e. Blanking of part of the tail by the body is a sec­ond effect, and a reduction of the relative wind when the tail lies in the wing wake is the third.

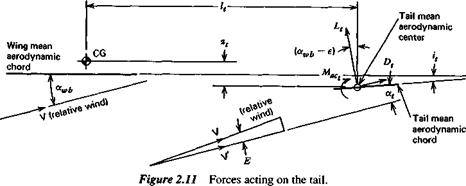
Figure 2.11 depicts the forces acting on the tail showing the relative wind vector of the airplane. V’ is the average or effective relative wind at the tail. The tail lift and drag forces are, respectively, perpendicular and parallel to V’. The reader should note

the tail angle /„ which must be positive as shown for equilibrium. This is sometimes referred to as longitudinal dihedral.

The contribution of the tail to the airplane lift, which by definition is perpendicu­lar to V, is

L, cos e — D, sin e

e is always a small angle, and we assume that Dte may be neglected compared with Lt. The contribution of the tail to the airplane lift then becomes simply L,. We intro­duce the symbol CLt to represent the lift coefficient of the tail, based on the airplane dynamic pressure |pV2 and the tail area S,.

L,

lpV2S,

The total lift of the airplane is or in coefficient form

Cl = Cu, + j CL, (2.2,6)

The reader should note that the lift coefficient of the tail is often based on the local dynamic pressure at the tail, which differs from |pV2 when the tail lies in the wing wake. This practice entails carrying the ratio V’/V in many subsequent equations. The definition employed here amounts to incorporating V’/V into the tail lift-curve slope a,. This quantity is in any event different from that for the isolated tail, owing to the interference effects previously noted. This circumstance is handled in various ways in the literature. Sometimes a tail efficiency factor 17, is introduced, the isolated tail lift slope being multiplied by 17,. In other treatments, 17, is used to represent (V’/V)2. In the convention adopted here, a, is the lift-curve slope of the tail, as measured in situ on the airplane, and based on the dynamic pressure pV2. This is the quantity that is directly obtained in a wind-tunnel test.

From Fig. 2.11 we find the pitching moment of the tail about the CG to be

M, = —l,[L, cos (awb – є) + D, sin (awh – є)]

– z,[D, cos (awh – e) – L, sin (awb – e)] + Mai. (2.2,7)

Experience has shown that in the majority of instances the dominant term in this equation is the first one, and that all others are negligible by comparison. Only this case will be dealt with here. The reader is left to extend the analysis to cases in which this approximation is not valid. With the above approximation, and that of small an­gles,

M, = – I A = —l, CL£pV2S,

Upon conversion to coefficient form, we obtain

The combination l, S,/Sc is the ratio of two volumes characteristic of the airplane’s

geometry. It is commonly called the “horizontal-tail volume ratio,” or more simply, the “tail volume.” It is denoted here by VH. Thus

cm, = – VHCL, (2.2,9)

Since the center of gravity is not a fixed point, but varies with the loading condi­tion and fuel consumption of the vehicle, VH in (2.2,9) is not a constant (although it does not vary much). It is a little more convenient to calculate the moment of the tail about a fixed point, the mean aerodynamic center of the wing-body combination, and to use this moment in the subsequent algebraic manipulations. Figure 2.12 shows the relevant relationships, and we define

– Is,

VH=~ (2.2,10)

cS

which leads to

V„=VH – j(h~hnJ (2.2,11)

The moment of the tail about the wing-body mean aerodynamic center is then [cf.

(2.2,9) ]

C„„ = ~V„CL, (2.2,12)

and its moment about the CG is, from substitution of (2.2,11) into (2.2,9)

Cm, = – VHCL, + CLt j(h – hnJ (2.2,13)