Non-dimensionalization

Non-dimensionalization can be viewed as the process of converting from standard to natural units. We can define all coordinates and field variables in terms of dimensionless variables () and the various natural units or scales listed in Table 1.1.

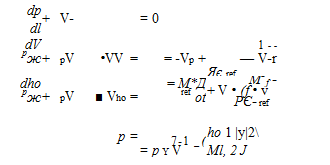Substituting these into the compressible mass, momentum, total enthalpy, and ideal-gas state equations (1.33), (1.36), (1.38), (1.13), gives the corresponding dimensionless equations. The body force f and volume heating qV are omitted here, since they are not relevant in typical aerodynamic flows.

Here V() = 4efV() is the gradient in terms of r derivatives, and r, q arc the non-dimensional viscous stress tensor and heat flux vector, defined using Д, It, VV, Vh0.

Equations (1.45)-(1.48) have the same form as their dimensional counterparts, except for the appearance of four non-dimensional parameters formed with the reference scales, as summarized in Table 1.2. For incompressible flows, discussed in more detail in Section 1.8, the enthalpy and state equations (1.47),(1.48) are replaced by the simple relation p = constant. In this case, only (1.45),(1.46) are needed to fully determine the V, p fields and the resulting aerodynamic forces. Hence the Reynolds number is the only relevant aerodynamic parameter for steady incompressible flows.