Pascal’s law

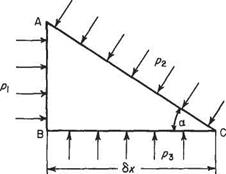
Consider the right prism of length 6z into the paper and cross-section ABC, the angle ABC being a right-angle (Fig. 1.2). The prism is constructed of material of the same density as a bulk of fluid in which the prism floats at rest with the face BC horizontal.

PressuresPi, P2 andрз act on the faces shown and, as proved above, these pressures act in the direction perpendicular to the respective face. Other pressures act on the end faces of the prism but are ignored in the present problem. In addition to these pressures, the weight W of the prism acts vertically downwards. Consider the forces acting on the wedge which is in equilibrium and at rest.

Fig. 1.2 The prism for Pascal’s Law

Resolving forces horizontally,

p (6x tan a)6z —p2(Sx sec a) 6z sin a = 0 Dividing by 6x 6z tan a, this becomes

pi – p2 = 0

i. e.

Pi = P2

Resolving forces vertically,

Рзбхбг — p2(6xssca) fecosa — W = 0

Now

W = pg(6x)2 tan a 6zj2

therefore, substituting this in Eqn (1.2) and dividing by 6x6z,

Ръ ~P2~jPg tan a 6z = 0

If now the prism is imagined to become infinitely small, so that <5jc —► 0 and 6z —у 0, then the third term tends to zero leaving

Ръ ~P2 = 0

Thus, finally,

Pl=P2=P3 (1.3)

Having become infinitely small, the prism is in effect a point and thus the above analysis shows that, at a point, the three pressures considered are equal. In addition, the angle a is purely arbitrary and can take any value, while the whole prism could be rotated through a complete circle about a vertical axis without affecting the result. Consequently, it may be concluded that the pressure acting at a point in a fluid at rest is the same in all directions.