Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
PATHLINES, STREAK LINES, AND STREAMLINES
Three sets of curves are normally associated with providing a pictorial description of a fluid motion: pathlines, streak lines, and streamlines.
Pathlines. A curve describing the trajectory of a fluid element is called a pathline or a particle path. Pathlines are obtained in the Lagrangian approach by an integration of the equations of dynamics for each fluid particle. If the velocity field of a fluid motion is given in the Eulerian framework by Eq. (1.4) in a body-fixed frame, the pathline for a particle at P0 in Fig. 1.1 can be obtained by an integration of the velocity. For steady flows the pathlines in the body-fixed frame become independent of time and can be drawn as in the case of flow over the airfoil shown in Fig. 1.1.
Streak lines. In many cases of experimental flow visualization, particles (e. g., dye, or smoke) are introduced into the flow at a fixed point in space. The line connecting all of these particles is called a streak line. To construct streak lines using the Lagrangian approach, draw a series of pathlines for particles passing through a given point in space and at a particular instant in time, connect the ends of these pathlines.
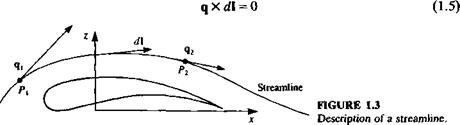
Streamlines. Another set of curves can be obtained (at a given time) by lines that are parallel to the local velocity vector. To express analytically the equation of a streamline at a certain instant of time, at any point P in the fluid, the velocity* q must be parallel to the streamline element dl (Fig. 1.3). Therefore, on a streamline:
|
|
Bold letters in this book represent vectors.
If the velocity vector is q = (a, v, w), then the vector equation (Eq. (1.5)) reduces to the following scalar equations:
w dy – v dz = 0 и dz —wdx = 0 v dx — и dy = 0
or in a differentia] equation form:
dx _dy _dz и v w
In Eq. (1.6a), the velocity (a, v, w) is a function of the coordinates and of time. However, for steady flows the streamlines are independent of time and streamlines, pathlines, and streak lines become identical, as shown in Fig. 1.1.
