PROBABILITY PROPERTIES OF RANDOM VARIABLES

An important goal in the study of random processes is to predict the probability of a given event—for example, in flight through turbulence, the occurrence of a given bank angle, or vertical acceleration. In order to achieve this aim, more information is needed than has been provided above in the spectral representation of the process and we must go to a probabilistic description.

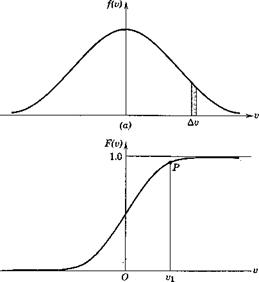
Consider an infinite set of values of v(tf) sampled over an infinite ensemble of the function. The amplitude distribution or probability density of this set is then expressed by the function f(v), Fig. 2.8a, defined such that the lim f{v) Av is the fraction of all the samples that fall in the range Av.

Av—>®

This fraction is then given by the area of the strip shown. It follows that

The cumulative distribution is given by

(2.6,24a)

and is illustrated in Fig. 2.86. The ordinate at P gives the fraction of all the samples that have values v < The distribution that we usually have to deal with in turbulence and noise is the normal or Gaussian distribution, given by

(2.6,25)

where a is the standard deviation or variance of v, and is exactly the rms value used in (2.6,8) = v (2.6,26)

Note that a can be computed from either the autocorrelation (2.6,7) or the spectrum function (2.6,11).