Results on Modified Grids

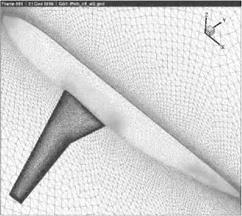
As a more realistic test case, the flow around the DLR-F6 model has been taken. The initial grid was prepared with the Centaur grid generation tool [3], see Fig. 13.

The simulation was done for Mach number of Ma = 0.75, an angle of attack of a = 0.00, using the Spalart-Almaras turbulence model in the original version (SAO). After the simulation on the initial grid was fairly converged, the adaptation was performed to increase the point number by 50%, using differences of the solu­tion gradients for refinement indication and using various values of the modification parameter. The modification parameter defines the portion of elements which is con­sidered for only regular refinement. In the test series it was increased from a value of 0, i. e. no modification, to a value of 0.1, the maximum value allowed. Table 3

shows the different modification parameter values, the actually inserted percentage of new points and how much of these new points are inserted by the edge indicator.

Table 3 List of tested modification parameter values, i. e. the portion of elements prepared for only regular refinement, the actual increase of the adapted grid and the portion of new points which was inserted by the initial edge refinement (and not by the modification) modification parameter 0.000 0.001 0.002 0.005 0.010 0.020 0.050 0.100 new points in % 49.95 50.02 50.10 50.03 50.31 50.26 50.40 50.47 portion of new points initially inserted in % 100.0 95.26 93.85 90.85 86.66 78.37 49.49 10.60

With an increasing influence of the modification, i. e. with a larger number of elements considered for regular refinement only, the portion of points inserted by indicators decreases, because a lot of points are needed for the regular refinement of badly shaped elements. The table shows that increasing the modification parameter beyond 0.05 seems to be not a reasonable choice in this example, because the ratio of points spent for adaptation of the grid resolution and points spent for the quality manipulation is too small.

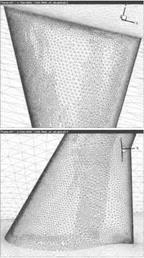
The differences of the surface grids for the unmodified case and the case using the modification parameter 0.01 also show this effect, see Fig. 14. In the modified case less points are used to refine the area of the shock system. These points are moved to some badly shaped elements to improve their subdivision. Because these changes mostly are done locally at places where refinement already occured in the unmodified case, it is hard to find them in the picture. They are located in the areas of the wing-body intersection and behind the trailing edge. In these areas probably the convex or concave geometry forced the grid generation tool to introduce some elements of lower quality.

The results for the integrated lift and drag coefficents and the residuals after 2000 and 10000 solver iteration steps after the adaptation are listed in the table 4. The results are compared to the corresponding results on a globally refined grid. The globally refined grid includes all the refinements that any local adaptation could do, and the element quality is perfectly preserved because all subdivisions are regular. So the result on the globally refined grid are the best what a local adaptation is able to achieve. The grey-shade of the entries indicates if the result is more accurate or smaller in case of a residual than the corresponding value for the unmodified case. Black entries are better, grey entries are worse than the value of the unmodified case. In this example the best results are achieved with a modification parameter of

0. 005-0.010.

Another test example was a simulation on a Solar [8] grid for the HiReTT model. The initial grid has 3.61 million points and consisists of 3.16 million hexahedra, 25675 prisms, 81396 pyramids and 2.27 million tetrahedra. The calculation was

Table 4 Residuals and results of various adaptation modifications for the DLR-F6 model

modif. Ref. 0.000 0.001 0.002 0.005 0.010 0.020 0.050 0.100

param.

Res. 12k 6.864e-4 7.452e-4 7.185e-4 7.012e-4 5.244e-4 5.616e-4 6.114e-4 8.682e-4

Res. 20k 4.533e-5 4.466e-5 4.507e-5 4.452e-5 4.689e-5 4.627e-5 4.516e-5 5.302e-5

CL 4.581e-1 4.613e-1 4.610e-1 4.606e-1 4.594e-1 4.591e-1 4.597e-1 4.663e-1 4.656e-1

CD 2.665e-2 2.730e-2 2.728e-2 2.728e-2 2.727e-2 2.728e-2 2.727e-2 2.723e-2 2.721e-2

Table 5 Residuals and results of various adaptation modifications for the HiReTT model modif. param. Initial Global 0.000 0.002 0.005 0.010 0.020 new points in % 102.07 103.28 96.39 100.18 97.28 portion of new p. initially inserted 71.77 70.93 69.31 66.69 57.93 Res. 4000 8.621e-6 8.775e-6 8.816e-6 8.167e-6 6.601e-6 Res. 6000 1.354e-6 1.339e-6 1.320e-6 1.271e-6 1.128e-5 Cl 2.156e-1 2.143e-1 2.146e-1 2.146e-1 2.144e-1 2.145e-1 2.144e-1 Cd 1.024e-2 9.941e-3 9.962e-3 9.962e-3 9.962e-3 9.964e-3 9.971e-3

done for a Mach number of Ma = 0.85, an angle of attack of a = 0.0°, using the Spalart-Allmaras turbulence model in the original version. After 3000 solver itera­tion steps the grid was adapted with 100% new points, using the differences of the primitive variables as the refinement indicator. Again, the adaptation was applied using the standard version and various values of the modification parameter.

Table 5 summarizes the results of the adaptation and the following calculation. In this example the best result is achieved for a modification parameter of 0.005. In this case the lift coefficient is approximated a little better, and the deviation of the drag coefficient is not increased.

Some more test calculations for the LANN-wing and the HIRENASD-wing con­sidering the modified adaptation were done. Summarizing the experiences from all tests performed until now, the following remarks can be made:

1. The influence of the described adaptation modification on the results of integral lift and drag coefficients is small compared to the influence of other parameters, e. g. the number of grid points or the turbulence model.

2. The results are almost never worsened for small values of the modification para­meter compared to the results using the unmodified adaptation.

3. The results get worse or unpredictable, if the modification parameter approaches the maximum value of 0.1.

4. The influence of the adaptation modification seems to be larger when introducing fewer («50%) new points than more («100%) new points in one adaptation step.

5. The residuals tend to fall faster for larger modifications in the first (1000-2000) solver steps after adaptation.

6. If the computation converges well, the residuals for smaller grid modification are often smaller than that for larger grid modification for the converged solution.

The reasons for the unexpected small influence on the results by this adaptation op­tion may be manifold. One possible explanation is that the element shape is less important for the local discretization error than the resolution of the considered examples and grid types. Another interpretation is that the red-green refinement strategy of the TAU adaptation is well suited for the considered grids, i. e. the loss

of element quality in bridging refinements does not affect the solution very much. See Sect. 6 for conclusions regarding the application.