Special Cases of Joukowski Airfoils

1.8.1 The Ellipse at Zero Incidence

Consider the circle centered at the origin and of radius b > a in the cylinder plane. Its image in the physical plane, through the Joukowski transformation, Eq. (2.39), is an ellipse centered at the origin, with main axis along Ox, from -2a to 2a and with parametric representation

x = b~+a2 cos в = 2 cos в z = bl-a2 sin в = 2 sin в

where в represents the polar angle in the cylinder plane. The ellipse has thickness e (small axis) and chord c (large axis). The potential function in the cylinder plane is

and the velocity components are

дФ b2 1 дФ b2

Vr = 17 = U 1 – 72 cosв, ув = r — = – U 1 + ^ sinв (2.63)

On the surface of the cylinder, this reduces to

Vr = 0, Ув = -2U sin в (2.64)

Using the chain rule

І

дФ ___ дф dx і дф ді_

dr дx дг + дz дг

дФ _ дф д£ , дф 3z

дв = дx дв + дz дв

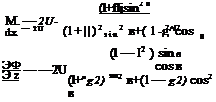(2.66)
the partial derivatives Ц – and дфф can be solved for, on the ellipse as
(2.67)
V U
(2.69)
N