Summary of Chapter 2

In this Chapter, mathematical solutions are found analytically for a theoretical model of steady, two-dimensional, inviscid, incompressible, adiabatic flow with uniform upstream conditions. This flow has no vorticity. The governing first order partial dif­ferential equations (Cauchy/Riemann system) for the velocity components are linear, representing conservation of mass and the irrotationality condition. The pressure is decoupled and is obtained from Bernoulli’s law.

The Cauchy/Riemann system can be replaced by a single potential or stream – function equation which satisfies Laplace equation. The uniform flow is a trivial
solution of these equations. Other fundamental solutions are found (i. e. source/sink and potential vortex) and more general solutions are constructed via superposition, for example doublet and half-body flows.

The solution for the flow over a circular cylinder is of particular interest. The boundary conditions are the tangency condition at the solid surface and uniform flow in the far field. From symmetry, the cylinder has zero lift and zero drag. The latter result is referred to d’Alembert Paradox. In the real flow, there is drag due to friction and due to the difference in pressure on the front and the back of the cylinder because of separation. However, this mathematical solution is useful since it provides the pressure distributions over thin bodies at small angle of attack via mapping techniques. For example, the Joukowski transformation provides analytical solutions for a family of symmetric shapes. In such cases, the flow is attached and the viscous effects are confined to the thin boundary layers, hence the mathematical model of inviscid flow yields a reasonable approximation.

A more interesting case is the flow with lift. Flow asymmetry is necessary to generate lift. One can think of a rotating cylinder. In the real flow, the effect of the rotation of the cylinder is transmitted through a viscous layer, augmenting the velocity on one side and retarding it on the other, thus creating a circulatory flow and lift. The inviscid flow model however, admits a slip velocity at the surface and has no mechanism to control the asymmetry other than adding a small flap to force flow stagnation at a specified point on the surface of the cylinder. The mathematical solution is obtained as uniform flow plus a doublet and a potential vortex. The doublet strength is determined to satisfy the tangency condition at the cylinder surface. In general the mathematical solution is not realistic since there is flow separation (unless the cylinder rotates so fast that the boundary layer is confined to a thin annulus attached to the surface). Through the Joukowski transformation however, the solution can be mapped to a flow over a lifting airfoil. To obtain a solution consistent with the experimental results, at least for small angles of attack when the flow is attached and the viscous effects are confined to thin boundary layers, the circulation in the mathematical model is chosen such that the flow leaves the trailing edge smoothly, in a direction bisecting the trailing edge angle. This celebrated Kutta-Joukowski condition renders the mathematical solution unique by choosing the most physically relevant solution which has no flow around the trailing edge, since in a real flow, the viscous effects will not allow such a behavior.

Once the vortex strength is determined, the lift is calculated via the Kutta – Joukowski lift theorem which is based on momentum balance. The same result can be obtained by integrating the surface pressure.

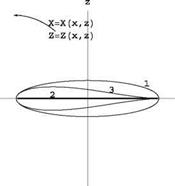
The Kutta-Joukowski transformation has allowed us to obtain exact solutions for the flow past ellipses, flat plates and Joukowski airfoils. The circles in the cylinder plane and their images in the physical plane are shown for example in Fig. 2.29.

Finally, the main formulae in this chapter are the Kutta-Joukowski lift theorem result L’ = pUГ and the relation between the strength of the potential vortex and the position of the stagnation points on the cylinder. Through the Joukowski transformation, these formulae reveal the dependence of the lift on the angle of attack for a family of airfoils.

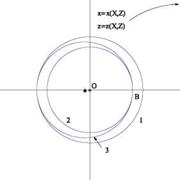Fig. 2.29 Circles 1,2 and 3 in the cylinder plane and their images: 1 ellipse, 2 flat plate, 3 Joukowski profile

In the next chapter, thin airfoil theory is introduced. The same results can be obtained numerically, using for example the method of singularities.

More accurate analyses, where the viscous effects in the boundary layer are fully accounted for, are presented later. Also, compressibility and three-dimensional effects are dealt with in separate chapters.