The Thermal State of the Surface and Thermal Surface Effects

The influence of, for instance, the Mach number or the Reynolds number on the appearance and kind of flow phenomena is well known and can be found everywhere in the text books. Mach number, Reynolds number and other “numbers” are similarity parameters, Chapter 4. Often overlooked is that the ratio ‘wall temperature’ to, for instance, ‘free-stream temperature’ (Tw/Тж) is also a similarity parameter, Section 4.4. In the text books one finds in this regard, with a few exceptions, usually at most that the wall temperature influences the skin friction, often in combination with the Mach number, and for the adiabatic wall only [23].

The classical wind tunnel experiment regarding heat loads is made with a cold model wall, often with an uncontrolled surface temperature. The task of the experiment is to find the distribution of the Stanton number and nothing more. This is the Stanton-number concept: the heat flux in the wall qw is specified basically by the—on the whole model surface in general constant— difference of the recovery temperature Tr and the wall temperature Tw.[9] The heat flux in the wall is equal to the heat flux in the gas at the wall: qw = qgw.

At the radiation cooled surface of an hypersonic flight vehicle the situation is different. The wall temperature Tw basically is due to the balance of three heat fluxes: the heat flux in the gas at the wall qgw, Sub-Section 4.3.2, the radiation-cooling heat flux qrad, Sub-Section 3.2.1, and the heat flux in the wall qw, Section 3.1. Other heat fluxes may be of importance, too: surface – tangential heat fluxes, heat fluxes due to non-convex effects, and to shock – layer radiation. Because the different fluxes are functions of the location on the vehicle’s surface, the resulting wall temperature is a function of the surface location, too.

For hypersonic flight vehicles the actual wall temperature Tw and the temperature gradient in the gas normal to the vehicle surface dT/dngw are of large importance. We call them together the “thermal state of the surface”. This state influences not only thermal loads, but also viscous and thermo­chemical flow phenomena at and near the vehicle surface (external and in­ternal flow paths). We call this influence “thermal surface effects”. Both the concept of the thermal state of the surface and the concept of thermal surface effects are important topics of this book.

The influence of the Mach number, the Reynolds number and other simi­larity parameters on the flow can qualitatively be discussed by looking at the orders of magnitude of the numbers. Take for instance the Mach number, which indicates compressibility effects in the flow, page 92. For M ^ 1 we speak of incompressible flow, at M « 1 we have the transonic regime and so on. Similarly we can make an ordering of viscous transport phenomena by looking at the relative magnitude of the Reynolds number, page 92.

Regarding the thermal surface effects, the situation is complicated. A simple ordering of effects is not possible. The influence of the thermal state of the surface on viscous and thermo-chemical surface effects of course is additional to that of the basic parameters Mach number, Reynolds number, stream-wise and cross-wise pressure gradients, etc. In several of the follow­ing chapters we show and discuss some examples of viscous thermal surface effects. Eventually we devote Chapter 10 to a deeper discussion of further examples. Examples of thermo-chemical thermal surface effects cannot be considered in the frame of this book.

We define now the thermal state of the surface and the thermal surface effects in a formal manner.

The Thermal State of the Surface. Under the “thermal state of the sur­face” we understand the temperature of the gas at the surface (wall temper­ature), and the temperature gradient, respectively the heat flux, in it normal to the surface [24].[10] As will be shown in Chapter 3, these are not necessarily those of and in the surface material. Regarding external surfaces we note, that these are, with some exceptions, in general only radiation cooled, if we consider RV’s or CAV’s and ARV’s flying in the Earth atmosphere at speeds below approximately 8 km/s [14].

The thermal state of the surface thus is defined by

— the actual temperature of the gas at the wall surface, Tgw, and the temper­ature of the wall, Tw, with Tgw = Tw, if low-density effects (temperature jump, Sub-Section 4.3.2) are not present,

— the temperature gradient in the gas at the wall, dT/dngw, in direction normal to the surface, respectively the heat flux in the gas at the wall, qgw, if the gas is a perfect gas or in thermo-chemical equilibrium, Chapter 5.[11] The heat flux qw is not equal to qgw, if radiation cooling is present, Section 3.1.

Surface radiation cooling implies that Tw, dT/dngw, qgw and qw are not constant over a vehicle’s surface. Partly large gradients appear in downstream direction and also in lateral direction.

If one considers a RV, the thermal state of the surface concerns predom­inantly the structure and materials layout of the vehicle, and not so much its aerodynamic performance, except in some instances the performance of aerodynamic trim and control surfaces [5]. This is because the RV flies a “braking” mission, where the drag—wave drag, form drag, however negligi­ble skin-friction drag—on purpose is large (blunt configuration, large angle of attack, Table 1.1). Of course, if a flight mission demands large down-range or cross-range capabilities in the atmosphere, this may change somewhat [5, 21].

The situation is different for an (airbreathing) CAV (or ARV in the air­breathing propulsion mode), which like any aircraft is drag-sensitive, and where viscous effects, which are affected strongly by the thermal state of the surface, in general play an important role, Table 1.2. This concerns the drag, the performance of trim and control surfaces, and the performance of ele­ments of the (airbreathing) propulsion system (inlet, boundary-layer diverter duct, nozzle) [21, 5].

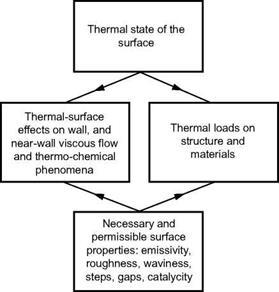
Thermal Surface Effects. This book puts emphasis on these facts by intro­ducing the concept of “thermal-surface effects”, which extends the classical “Stanton number” concept coming from the beginnings of high-speed flight. The Stanton number concept concerns mainly the classical thermal (heat) loads, which are of importance for the structure and materials concept of a vehicle. In contrast to that thermal-surface effects concern wall and near-wall viscous-flow and thermo-chemical phenomena, Fig. 1.4. This holds for both the external and the internal flow path of a flight vehicle.

Fig. 1.4. The thermal state of the surface and its different aero-thermal design implications.

A good understanding of thermal-surface effects is deemed to be necessary in design work for hypersonic flight vehicles, in particular CAV’s and ARV’s. Thermal-surface effects regard both the external and the internal flow path. Special attention must be given to tests in ground-simulation facilities, where usually cold-wall models are employed. The “hot experimental technique” is more or less in its infancy. Where it cannot be realized, extremely demanding other approaches may become necessary in order to fulfill ground verification needs of hypersonic flight vehicles or airbreathing propulsion systems [21].

Both thermal-surface effects and thermal loads are coupled directly to the necessary and permissible surface properties, which were mentioned in Section 1.3.

In the following Table 1.3 wall and near-wall viscous-flow and thermo­chemical phenomena as well as structure and materials issues are listed, which are influenced by the thermal state of the surface.

Table 1.3. Wall and near-wall viscous-flow/thermo-chemical phenomena, and structure and materials issues influenced by the thermal state of the surface (n is the direction normal to the surface, ( ) indicates indirect influence). Item Tw dT/dngw dT/dnw Boundary-layer thicknesses (<5, …) X Skin friction X Heat flux in the gas at the wall qgw X X Surface-radiation heat flux qrad X X (X) Laminar-turbulent transition X X Turbulence ? ? Uncontrolled/controlled flow separation X Shock/bondary-layer interaction X Hypersonic viscous interaction X Catalytic surface recombination X (X) Transport properties at/near the surface X X Wall heat flux qw X (X) X Material strength and endurance X Thickness of TPS or internal insulation X X (time integral of qw)

These encompass, for instance, the increase of the boundary-layer thick­ness, the displacement thickness, the thickness of the viscous sub-layer which governs turbulent skin friction and heat transfer, etc., with increasing wall temperature.

Lowered is the skin friction with increasing wall temperature, for turbu­lent flow stronger than for laminar flow. Increased is the separation disposi­tion with increasing wall temperature. The stabilization/destabilization and the laminar-turbulent transition of the boundary layer depends on both the

temperature gradient in the gas at the wall and the wall temperature. In­fluenced too are wall heat flux, shock wave/boundary-layer interaction, and hypersonic viscous interaction. The latter two, like flow separation, becoming more pronounced with increasing wall temperature. Catalytic surface recom­bination depends on the wall temperature, too.

Regarding materials and structures we note first of all that “thermal loads” encompasses both the wall temperature Tw and the wall heat flux qw. The wall temperature Tw governs the choice of surface material (and coating) in view of strength and endurance (erosion), and dT/dnw, respec­tively the flight-time integral of qw the thickness of the thermal protection system (TPS) of a RV [5].