Thermodynamic properties

Heat, like work, is a form of energy transfer. Consequently, it has the same dimen­sions as energy, i. e. ML2T-2, and is measured in units of Joules (J).

Specific heat

The specific heat of a material is the amount of heat necessary to raise the tempera­ture of unit mass of the material by one degree. Thus it has the dimensions L2T-20_1 and is measured in units of Jkg-1 °С-1 or Jkg_I K-1.

With a gas there are two distinct ways in which the heating operation may be performed: at constant volume and at constant pressure, and in turn these define important thermodynamic properties.

Specific heat at constant volume If unit mass of the gas is enclosed in a cylinder sealed by a piston, and the piston is locked in position, the volume of the gas cannot change, and any heat added is used solely to raise the temperature of the gas, i. e. the head added goes to increase the internal energy of the gas. It is assumed that the cylinder and piston do not receive any of the heat. The specific heat of the gas under these conditions is the specific heat at constant volume, cv. For dry air at normal aerodynamic temperatures, су = 718 J kg-1 K-1.

Internal energy (E) is a measure of the kinetic energy of the molecules comprising the gas. Thus

internal energy per unit mass E = cyT

or, more generally,

Specific heat at constant pressure Assume that the piston referred to above is now freed and acted on by a constant force. The pressure of the gas is that necessary to resist the force and is therefore constant. The application of heat to the gas causes its temperature to rise, which leads to an increase in the volume of the gas, in order to maintain the constant pressure. Thus the gas does mechanical work against the force. It is therefore necessary to supply the heat required to increase the temperature of the gas (as in the case at constant volume) and in addition the amount of heat equivalent to the mechanical work done against the force. This total amount of heat is called the specific heat at constant pressure, cp, and is defined as that amount of heat required to raise the temperature of unit mass of the gas by one degree, the pressure of the gas being kept constant while heating. Therefore, cp is always greater than cv. For dry air at normal aerodynamic temperatures, cp = 1005 J kg-1 K-1.

Now the sum of the internal energy and pressure energy is known as the enthalpy (h per unit mass) (see below). Thus

h = cpT

Entropy Entropy is a function of state that follows from, and indicates the working of, the second law of thermodynamics, that is concerned with the direction of any process involving heat and energy. Entropy is a function the positive increase of which during an adiabatic process indicates the consequences of the second law, i. e. a reduction in entropy under these circumstances contravenes the second law. Zero entropy change indicates an ideal or completely reversible process. By definition, specific entropy (5)* (Joules per kilogram per Kelvin) is given by the integral

It should be remembered that this result is obtained from the equation of state for a perfect gas and the equation of conservation of energy of the flow of a non-heat­conducting inviscid fluid. Such a flow behaves isentropically and, notwithstanding the apparently restrictive nature of the assumptions made above, it can be used as a model for a great many aerodynamic applications.

(1.25)

for any reversible process, the integration extending from some datum condition; but, as seen above, it is the change in entropy that is important, i. e.

T

(1.26)

In this and the previous equation dQ is a heat transfer to a unit mass of gas from an external source. This addition will go to changing the internal energy and will do work. Thus, for a reversible process,

dQ = d£ + pd 1^- dg = cvdT pd{/p) j j I j

(1.27)

but p/T = Rp, therefore

(128) Integrating Eqn (1.28) from datum conditions to conditions given by suffix 1, Si = си1п-5- + Д1п^ Ти pi

Likewise,

S2 = cvu^+ Ru^ Ти Pi

* Note that in this passage the unconventional symbol S is used for specific entropy to avoid confusion with the length symbols.

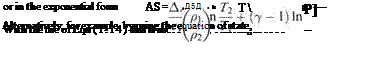and the entropy change from conditions 1 to 2 is given by

(1.32)

These latter expressions find use in particular problems.