Aerodynamics of Hovering Flight

MOMENTUM METHOD

Basis of the Theory

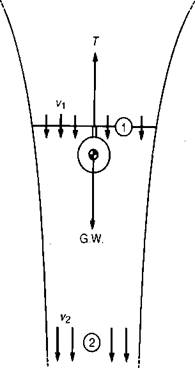
Like any physical system, the hovering helicopter must obey the basic laws of physics. One of these laws was stated by Newton: "For every action, there is an equal and opposite reaction.” In the case of the helicopter in hovering flight, the action is the development of a rotor thrust equal to the gross weight. The reaction

In the subsequent text, there are a number of times when some light can be shed on the theory by using specific numerical examples. For this purpose, a typical helicopter has been defined and designated the example helicopter. The characteristics of this aircraft are listed in Appendix A.

®v0

is represented by the acceleration of a mass of air from a stagnant condition far above the rotor to a condition with a finite velocity in the wake below the rotor, as shown in Figure 1.1. The conditions at the rotor are governed by the familiar relationship:

Force = (Mass) (acceleration)

For systems such as rotors that are accelerating a mass of air on a continuous basis, the equation may be written as:

Rotor Thrust = (Mass flow per second) (total change in flow velocity)

or:

T = (яг/sec) (Д?)