AUTONOMOUS LINEAR/INVARJANT SYSTEMS

The general equation for linear/invariant systems is (3.2,20). When the system is autonomous and hence has zero input it reduces to

У = Ay (3.3,1)

When the initial state vector is y(0), the Laplace transform of (3.3,1) is

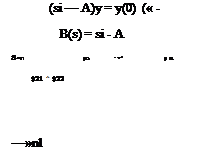sy = Ay + y(0)

in which atj are the elements of A. В is called the characteristic matrix of the system. Equation (3.3,2) then becomes

	B(s)y = y(0)
whence	у = B-!(s)y(0)	(3.3,4)
where	B-i-adiB |B|	(3.3,5)

By virtue of the definition of the adjoint matrix (ref. 2.1) it is evident that the elements of adj В and of |B| are polynomials in s. |B| is called the char­acteristic determinant, and its expansion

|B| =/(e) (3.3,6)

is the characteristic polynomial. It is evident from (3.3,3) that /(s) is of the

nth degree. Hence

f(s) = sn + cn_1sn~’1 H——– c0

= (s – ^)(s -*,)•••(«- K) (3.3,7)

where • ).n are the roots of /(s) = 0, the characteristic equation. We now rewrite (3.3,4) as

l(s) = ~^-У(0) (3-3,8)

f(s)

The inversion theorem (2.5,6) can be applied to (3.3,8) for each element of y, and the column of these inverses is the inverse of y(s), i. e.

УV) = I P B(S)) y(0)eA,<

r=l l f(s) }s=xr

We now define the vector

and hence can write the general solution of (3.3,1) that satisfies the initial conditions as

. У« = І>е^ (3.3,10)

r~ 1

n

It follows that y(0) = 2 Уr Note also that by setting t = 0 in (3.3,9) the

r=l

summation therein is shown to be equal to the identity matrix I.

COMPACT FORM OF SOLUTION

A more compact form of the solution is available. Define the exponential function of a matrix M by an infinite series (like the ordinary exponential of a scalar), i. e.f

eM=I + M + – M2 + — –

2!

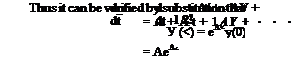It is evident then that

is a solution of (3.3,1) that has the initial value y(0).