Autorotation

Notice that from the universal power curve in Fig. 2.20 there is actually a value of Vc/vh for which zero net power is required for the rotor [i. e., P — T(VC + Vi) = 0 or P/Ph = 0]. This condition is called ideal autorotation for vertical flight. For a given thrust it is a self-sustained operating state where the energy to drive the rotor comes from potential energy converted to kinetic energy from the relative descent velocity (which is upward relative to the rotor). The principle of autorotation can be seen in nature in the flight of sycamore or maple seeds, which spin rapidly as they slowly descend and are often carried on the wind for a considerable distance. In practice an autorotation is a maneuver that can be used to recover the helicopter to the ground in the event of an engine failure, transmission problems, or loss of the tail rotor. It requires that the pilot let the helicopter descend at a sufficiently high but controlled rate, where the energy to drive the rotor can be obtained by giving up potential energy (altitude) for energy taken from the relative upward flow through the rotor, thereby averting a ballistic fall.

On the basis of assuming the validity of Eq. 2.94, it will be apparent that the power curve crosses the ideal autorotation line Vc + и,- = 0 at

(2.100)

which gives Vc/Vh = — 1.75 for an ideal rotor (к = 1). In practice, areal (actual) autorotation in axial flight occurs at a slightly higher rate than this, because in addition to induced losses at the rotor, there are also a proportion of profile losses to overcome. In a real autorotation we can write

P=fcT(Vc + Vi)+P0=0.

Therefore, in a stable autorotation an energy balance must exist where the decrease in potential energy of the rotor TVC just balances the sum of the induced {kTvO and profile

:W3/2

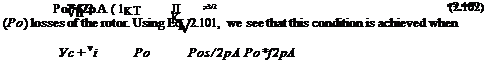which depends primarily on the disk loading. Also, using the definition of figure of merit (and assuming the induced and profile losses do not vary substantially from the hover values), then Johnson (1980) shows that

Using Eq. 2.94 for the induced velocity with Eq. 2.103 gives the real autorotation condition:

The first term on the right-hand side of Eq. 2.104 will vary in magnitude from —0.04 to —0.09, depending on the rotor efficiency. Compared to the second term, the extra rate of descent required to overcome profile losses is relatively small. Therefore, on the basis of the foregoing, it is apparent that a real vertical autorotation will occur for values of Vc/vh between —1.85 and —1.9, that is, according to Fig. 2.20, with the rotor operating in the turbulent wake state. Under these autorotative conditions, the flow above the rotor is known from experimental tests to be relatively turbulent and to resemble that from behind a bluff body (see Question 2.15).

t+ ^ 4-^ г* _ ________ я,™,

it io iiu^i^auug tu тій uic ciictuvc uiag vucjlik;jlciu, £)eff, aciuig un me iuiaji 111 11110 nuw

state. We can equate the rotor thrust to its effective drag force using

T = w = pV^acDm.

Now in hover we know that T = 2pAv, so solving for Cotff for the autorotational condition Vc/vh ^ —1.9 gives

This is close to the drag coefficient of bluff bodies [see Hoemer (1965), where Co = 1.11 for a disk, Со = 1.2 for a closed hemisphere and Cd = 1-33 for an open hemisphere], which means that aerodynamically the rotor produces a resultant force equivalent to a parachute when in the autorotative state.

T 41 1 О •Р/Чіт/4 fll n 4- IT 74 4-1» rt 1-* ліїл nnfП1ТІГЧ*</4п^І /ЧМ П «VMl’nf Л M л *-l nf «</ч1 A – w Irtl T 7 Іч 4 ҐГІЧ

ii id luuiiu uiai wiui a ii^utupiu, auiuiuiauuiid uiudi иъ jj^iiuini^u ai i^iauv^ mgii

rates of descent. Using the result that Vh ^ 14.49^/TjA, where T/А is in lb/ft2, gives Vc & — 26.81 y/TjA ft s-1 for autorotation at sea level conditions, which for a representative disk loading of 10 lb ft-2 leads to a vertical rate of descent of about 5,000 ft min"1! However,, it is shown in later in Section 5.6 that with some additional forward speed, the power required at the rotor is considerably lower than in the hover case. Because autorotations involve an energy balance, the autorotative rate of descent can be reduced by about half with some forward airspeed, although in practice this is still a relatively high rate. Consequently, in an autorotation the proper recovery of the helicopter requires a high level of skill from the pilot. As the helicopter approaches the ground, the rotational kinetic energy
stored in the rotor can be used to arrest the rate of descent. To do this, the pilot will flare the helicopter using cyclic pitch (which helps to increase rotor rpm and stored rotational kinetic energy in the rotor) and then progressively increase the collective pitch so that the helicopter will settle onto the ground with minimum vertical and forward velocity. At this point, the rotational kinetic energy stored in the rotor will have been nearly exhausted and the rpm will have decayed to a low value. Clearly, the autorotative characteristics of the helicopter affect safety of flight and so autorotational capability becomes an important design issue. Autorotational flight performance is addressed further in Chapters 3, 5, and 6.