Biot-Savart Law

The three-dimensional velocity field associated with a vortex line is considerably more complicated and is given by the Biot-Savart law. The derivation of this law is beyond the scope of this text. Figure 2.15a illustrates

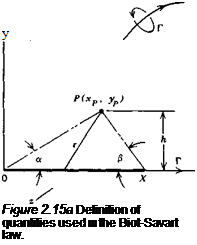Figure 2.15b The Biot-Savart law for a straight-line vortex.

a portion of a vortex line about which at any point the circulation, Г, is constant. If v, is the velocity vector induced at any point, P, in the field by the vortex line, the Biot-Savart law states

This is the most general form of the Biot-Savart law. dR is the derivative of the radius vector from the origin to the vortex line and is thus the directed differential distance along the line, r is the radius vector from the point P to the line element dR. The positive direction of the circulatory strength, Г, is defined according to the right-hand rule. The x, y, z orthogonal coordinate system is also right-handed.

A special form of the Biot-Savart law for a straight-line vortex segment found in many texts can be obtained by integrating Equation 2.63. Referring
to Figure 2.15b, for convenience the line vortex is placed on the x-axis and lies between 0 and x. The z-axis will project out of the paper according to the right-hand rule. The circulation Г is taken to be positive in the x direction which means it will be clockwise when viewed in that direction. For this figure,

R = ix
OP + r = R

OP = і xp + j yp

r = i(x-xP)-jyP dR = idx

so that

	‘ j	к
rx dR =	(х-Xp) – yp	0
	dx 0	0

= к yP dx

|r| = [_(x – Xp)2 + yp2]112

Equation 2.63 then becomes dx

V‘ ~ 4tt Jo [(x – Xp)2 + yP2]312

(2.64)

a, /3, and h are defined in Figure 2.15b. Notice that the velocity has only a z component. As the line becomes infinite in length, the angles a and j3 approach zero, and Equation 2.64 reduces to the expression for the velocity around a two-dimensional point vortex given by Equation 2.56.