Centre of pressure

The aerodynamic forces on an aerofoil section may be represented by a lift, a drag, and a pitching moment. At each value of the lift coefficient there will be found to be one particular point about which the pitching moment coefficient is zero, and the aerodynamic effects on the aerofoil section may be represented by the lift and the drag alone acting at that point. This special point is termed the centre of pressure.

Whereas the aerodynamic centre is a fixed point that always lies within the profile of a normal aerofoil section, the centre of pressure moves with change of lift coefficient and is not necessarily within the aerofoil profile. Figure 1.11 shows the forces on the aerofoil regarded as either

(a) lift, drag and moment acting at the aerodynamic centre; or

(b) lift and drag only acting at the centre of pressure, a fraction kCp of the chord behind the leading edge.

Then, taking moments about the leading edge:

Mle = Mc — (L cos a + D sin q:)xac = — {L cos a + D sin a)kcpc Dividing this by p Vі Sc, it becomes

giving

Again making the approximations that cos a ~ 1 and CD sin a can be ignored, the Eqn (1.54), above, becomes

(1.55)

At first sight this would suggest that kcp is always less than хде/с. However, CVAC is almost invariably negative, so that in fact fccp is numerically greater than jcac/c and the centre of pressure is behind the aerodynamic centre.

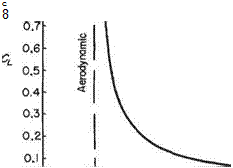
Example 1.5 For the aerofoil section of Example 1.4, plot a curve showing the approximate variation of the position of centre of pressure with lift coefficient, for lift coefficients between zero and unity. For this case:

kcp — 0.233 – (—0.04/Cl) ^ 0.233 + (0.04/Cl)

The corresponding curve is shown as Fig. 1.12. It shows that kcp tends asymptotically to хдс as CL increases, and tends to infinity behind the aerofoil as CL tends to zero. For values of CL less than 0.05 the centre of pressure is actually behind the aerofoil.

For a symmetrical section (zero camber) and for some special camber lines, the pitching moment coefficient about the aerodynamic centre is zero. It then follows, from Eqn (1.55), that kcp = хдс/с, i. e. the centre of pressure and the aerodynamic centre coincide, and that for moderate incidences the centre of pressure is therefore stationary at about the quarter-chord point.

l. l 1.0 0.9

0.8 •

0 O. l 0.2 0.3 0.4 0.5 0l6 0.7 0.8 0.9 1.0 l. l 1.2 1.3 1.4

ТЕ

Fig. 1.12 Centre of pressure position for Example 1.5