. Compressible Flow Quantities

The various thermodynamic definitions and relations derived in Chapter 1 will now be recast into forms suitable for compressible aerodynamic analysis.

8.2.1 Stagnation quantities

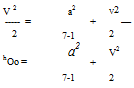The stagnation enthalpy or equivalently the total enthalpy, which was defined and treated in Chapter 1, is constant in an adiabatic flow and is These must also be constant and equal to their freestream values, but only in isentropic regions of the flow.

The known freestream total enthalpy in (8.3) also gives convenient alternative expressions for the local speed of sound and Mach number in terms of their freestream values and the local normalized speed V/Vo.

8.2.2 Isentropic static density and pressure

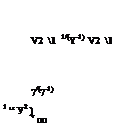Wherever po and Po are equal to the known freestream values, i. e. in isentropic regions of the flow, there we can express the static density and pressure only in terms of the Mach number or the velocity.

Since external aerodynamic analyses frequently employ the velocity potential, the velocity forms above will be the more useful ones here. Note that relation (8.10) is the same as the steady version of the compressible Bernoulli equation (1.112).

The definition of the pressure coefficient remains unchanged from the incompressible case, but its depen­dence on the Mach number or velocity is now different.

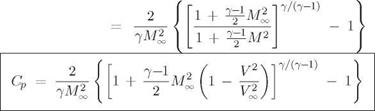(8.11)

(8.12)