Conclusion

The methods of adjoint error estimates and local mesh modification are applied to several test cases. The main focus was set on the global aerodynamic coefficients. Only for the mesh repairing the focus was set on the validity and the computablility of meshes.

For the adaptation series of the DLR-F6 with the adjoint error estimates no final conclusion can be given. The numerical values given by [12] are widely spread. The corresponding experimental data show for some coefficients improvements and for some not. At least one should note that a comparison of the experimental results for Re = 3 • 106 measured in the NASA NTF and in the ONERA S2MA facility shows as well differences especially in the drag [7]. If one projected these differences to the measurements at Re = 5 • 106 the adapted meshes would show an improvement for all coefficients.

However, the results of the adaptation series converge for both used sensors to similar values which are different from the values of the finest mesh. The results on the meshes which are locally modified to satisfy a quality measure based on an anisotropic metric are close to the results computed on the original meshes.

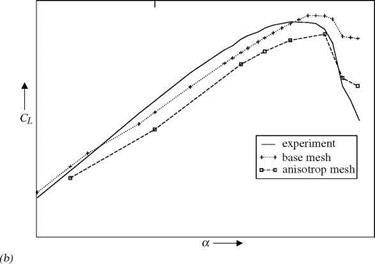
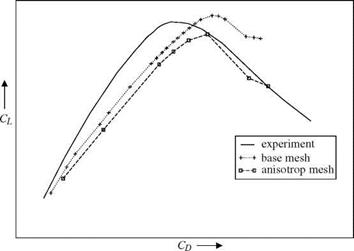
For the high-lift configuration the adjoint approach improves the results in the linear region of the polar. The values of maximal lift are ambiguous and depend on the used meshes. The deviations of the results on the meshes which are optimized to

(b)

(c)

an anisotropic quality measure increase. The reason for the strong deviations have to be analyzed.

The results for the adjoint approach show additionally that the strategy to use one grid for the whole polar works even if the adaptation was performed only for a specific angle of attack. This strategy reduces significantly the computational effort and makes the adjoint approach applicable.

The repairing of meshes was successfully demonstrated for several meshes. This method is useful if a computation on a mesh due to numerical errors or negative elements fails and a new mesh generation is not desirable.

3 Outlook

[13] couples the adjoint adaptation with the feature of anisotropy. He demonstrated that with this mixed approach the convergence of the coefficients is much faster than with an isotropic mesh adaptation. [13] states that the adjoint approach balances the inaccuracies which can occur by the anisotropic meshes and uses the positive effects of anisotropic meshes. This has to be tested with the present methods.

Additionally the introduced error estimation approach of [2] tries to reduce the error with respect to numerical dissipation terms. The original work of [13] tries to reduce the error with respect to the discretization itself. A comparison of both approaches would also be interesting.

Acknowledgements. The author is grateful to R. Heinrich and E. Elsholz for providing the shown test cases for the mesh repairing.