Continuum

Throughout this book, a continuum assumption is implicit, which means that no matter how small the fluid particle being considered, it is assumed to contain many molecules of the fluid or the gas such that the behavior of individual molecules is not important. Another way to say this is that the mean free path of the molecules (i. e., the distance between molecular collisions) is assumed to be small when compared with any length scale considered, such as a body length or diameter or an average airfoil-chord length—even if the length scale is infinitesimal.

Size of a Particle in the Continuum Model

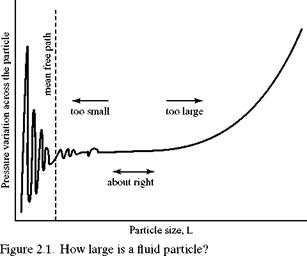
When applying the continuum idea, we often refer to the motion of a fluid particle, which represents an element of the medium that is small compared with the basic scale of the problem. For example, it could represent a particle of air moving over the surface of a wing. In that case, we assume that the particle is small compared with the distance traveled from the leading to the trailing edge—that is, the chord length. It is important to form an accurate picture of just how small the particle is. If it were the size of a molecule, then the concept of a continuum would fail because it would be necessary to account for individual molecular motion, as in the previous example. Figure 2.1 illustrates a “thought experiment” to select the correct size for a particle. Consider a particle in the form of a cubical box of finite length L on each side and imagine measuring the variation of a property of the fluid across the element. The pressure is a convenient property to use in this thought experiment. We want to choose a particle size such that the property in question exhibits a constant value throughout the element. Thus, if L were the chord length of the wing, it would not work because the pressure changes radically in moving from the leading to the trailing edge. As Fig. 2.1 shows, if L is too large, then there are large variations in the value of the property across the particle. Conversely, if the particle is too small (e. g., the size of a few molecules), then the concept of pressure is lost. There would be huge oscillations in the pressure, depending on how many molecules happened to be inside the test volume at a given instant. On this basis, it appears that a prac­tical lower limit for the size of a valid particle is a fairly large number of mean free paths, X.

We must ensure that there is a sufficient number of molecules in the particle so that the influence of individual molecular motion is “smoothed out.” Therefore, the practical answer to the question, “How large is a fluid particle?,” is “Very, very small, but not too small.”

Resolution of Aerodynamic Forces in Normal and Parallel Components

In addition to the pressure, other fluid properties are needed to model aerodynamic forces. In particular, the effects of energy dissipation or friction must be considered. In the simplest picture, forces normal to a surface are created by elastic molecular collisions. This simplified model suffices in some situations; however, the effects of forces parallel to the surface arising from viscous interactions can be of crucial importance in many aerovehicle-design problems.

Figure 2.2 illustrates the basic concept for resolving the interaction-force incre­ment at a point into components normal and parallel to the surface. Consider the force dF acting on a small area element, dA, at any location on the body shown. The normal component dFn most often is due to the action of pressure on an element of the surface:

dF„ = -(pdA)n. (2.2)

The negative sign indicates that the local pressure force acts toward the surface— that is, in a direction opposite to the outward-pointing unit normal vector, n. The pressure can be due to momentum exchange from both the random molecular motion (i. e., the thermodynamic pressure) and the directed motion of the particles due to flow of the gas in the continuum sense. The latter pressure component often is referred to as the dynamic pressure and is an important element in subsequent chap­ters, which discuss control of dynamic pressure by the shape and orientation of the body. This is crucially important in the generation and control of lift (e. g., on a wing surface in external flows) and in the production of thrust (e. g., in a ducted propulsion system with internal flow).