Dimensional Analysis

With the simple tools now at our disposal, we can gain considerable insight into the nature of aerodynamic forces and related flow-field effects. A powerful tool is the requirement for dimensional homogeneity. This makes it possible to uncover relation­ships between parameters without complete information about the actual physics of any underlying phenomena, which may not be known at the outset. The method we now construct has many applications, not the least important of which is the planning and implementation of experimental studies of complex aerodynamic phenomena.

We return now to the ideas expressed in Eq. 2.8. We expect that on the basis of our observations, the drag force is a function of several flow parameters and on the geometrical configuration of the object immersed in the gas flow. This is true for any aerodynamic force component, F, so let us generalize by writing:

F = F(V, p, p, a, d), (2.10)

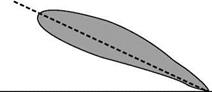
where we now have chosen a set of parameters that reflect our expectations that speed, V; gas density, p; and size may affect the force. We also include the speed of sound, a, and the coefficient of viscosity to account for possible compressibility and shear-force effects. The pressure is excluded because the force is clearly the result of pressure distribution over the body; to include it simply would double the depen­dence on the same quantity. The influence of the size of the object is reflected by inclusion of a length d, which could be any one of the dimensions of the object (e. g., length or width). A parameter describing the shape is not incorporated because it is not possible to represent this by a mathematical parameter. Instead, we employ the concept of geometric similarity. The relationship to be constructed holds for any family of objects, possibly of different sizes but with the same shape (as illustrated in Fig. 2.4)—that is, a family of similar shapes.

We now examine Eq. 2.10 from the standpoint of dimensional reasoning. The method to be used often is generalized in an elegant form known as the Buckingham Pi Theorem. The full machinery is not needed at this point in the discussion; a sim­pler intuitive approach is more instructive as an introduction.

The first step is to choose an appropriate mathematical form for the relation­ship implied in Eq. 2.10. To accomplish this, we simply note that in the majority of such situations, physical relationships involving several variables are in the form of products of powers of the several variables. There is no guarantee that this will work here; however, subject to subsequent careful analysis, we ask what such a relation­ship would yield in the current problem.

With this in mind, assume that the aerodynamic force F is a function of products of the several variables to unknown powers. This choice is based on the observation that mathematical descriptions of natural phenomena often take this form. Write:

F = CVc p°2 pc3 a°4 d°s,

Figure 2.4. Geometric similarity. All shapes shown are identical, although sizes are different. Because

(b)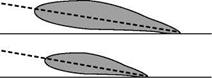

(a)-(c) also are oriented at the same angle to the reference line, they are geometrically similar.

(c) Shape (d) is identical to (a), but it is oriented differently with respect to the reference line. Therefore, shape (d) is not geometrically similar to the other shapes.

(d)

where C is an arbitrary (i. e., dimensionless) constant and cn (n = 1 to 5) is a set of initially undetermined exponents. Thus, in terms of the dimensions of each of the six factors, it is necessary for dimensional homogeneity that:

where the mass-based set defined in Table 2.2 is used. The same results would be forthcoming if the force-based dimensions were used instead. Now, for Eq. 2.11 to be dimensionally correct, it is necessary that each of the three basic units enters the problem with the same exponent on each side of the equation. Therefore, for dimen­sional homogeneity, it is necessary that 1

Therefore, the aerodynamic force can be written as:

F = СУ(2_Сз-С4)р(1-Сз)цСз a4 d(2-°3).

Collecting the terms with the same unknown exponent, we find:

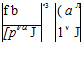
(2-14)

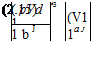It is not possible to determine the exponents c3 and c4 using dimensional homogeneity alone. However, the expression we found contains vital information regarding the dependence of the aerodynamic forces on the parameters that we identified as those most likely to matter. Notice that the expressions raised to the powers c3 and c4 are dimensionless groups of the variables. Because the exponents are unknown, it would be correct to rewrite Eq. 2.14 as:

where two new exponents (d3 and d4, which are obviously the negative values of the original two) are used. The two dimensionless groups clearly have physical significance in the system behavior. They are called similarity parameters and are the focus of considerable attention throughout this book. One of the param­eters, arising in a natural way in this simple analysis, is the Mach number V/a that was encountered in the introduction to compressibility effects previously in this chapter. The second, called the Reynolds number, clearly is related to effects of viscosity.