DLR-F6
This test case was defined for the Third AIAA CFD Drag Prediction Workshop [see 12]. The flow parameters for the DLR-F6 wing/body configuration are Ma « 0.75, Re « 5 • 106 and Tref = 322.22. The meshes were taken from the workshop[1].
The first test on this configuration is a comparison of a mesh refinement study and an adaptation series with the new sensors. For the refinement study a computation on a coarse (NP = 2464385), a medium (NP = 5102446) and a fine (NP = 8535263) mesh was performed. For all computations the lift is targeted to Cl = 0.5 and the Spalart-Allmaras turbulence model was used. Outgoing from the coarse mesh the adaptation was repeated five times with the new sensor given in equation (4). The number of points increases within each adaptation step by 30%. Additional to the flow computation in each adaptation step the adjoint error estimation was computed.
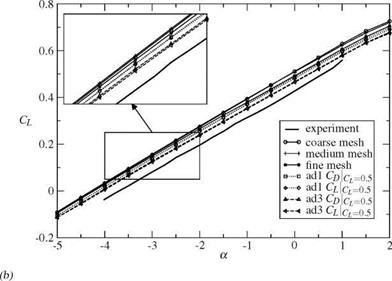
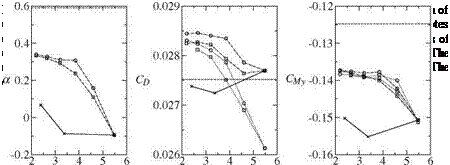
The values of the angle of attack a, the drag Cd and the pitching moment CMy of the refinement study are plotted in figure 3(a)-(c) as function of NP 2/3. The crosses show the results of the coarse, medium and fine mesh. The circles and squares connected by solid lines are showing the results of the adaptation with the new sensors for lift and drag, respectively. Signs connected by dotted lines denote values which are corrected by the adjoint error estimate (3). The results from the refined meshes show an ambiguous behaviour regarding the convergence for all plotted coefficients. In contrast the results from the adaptation series converge approximately to distinct values. The corrections by the adjoint error estimate decrease continuously so that finally the corrected values converge to the uncorrected values. The values of the finest meshes of the adaptation series are higher than the values from the finest mesh, e. g. ACd ~ 10DC.
A comparison with the results given in [12] shows that the results of the refined and of the adapted meshes are lying in the range of other codes. Additionally [12] make a statistical analysis of the values for drag. Their estimate for the mean of the drag is Cd = 0.0269, the standard deviation is о = 0.0006. Here the values of the adaptation are significantly out of this range.
The experimental results are taken from [7]. The measured values are shown in figure 3(a)-(c) by a dashed line. For the angle of attack and the pitching moment the adapted grids are lying closer to these experimental results than the results of the refined meshes. For the drag the values on the refined meshes are closer to the experiment.
In the second test a polar is computed. Again the flow conditions are Ma « 0.75, Re « 5 • 106 and Tref = 322.22°K. Instead of a fixed target lift coefficient here the angle of attack was varied in the range of a = [-5°, 2°]. The polar is computed on
the coarse, medium and fine mesh. To avoid the computation of an adjoint solution for each angle of attack, four adapted meshes from the previous adaptation series for lift and drag are used. Here the mesh from the first (ad1) and the third adaptation (ad3) step with NP « 3.2 • 106 and NP « 5.5 • 106 are chosen, respectively.
In figure 4(a) the lift is plotted as function of the angle of attack a. The results on the coarse, medium and fine mesh are denoted by о, + and *. On the coarse and medium mesh the results are similar. On the fine mesh the slope is lower than on the coarser meshes. The computed lift on the adapted meshes ad1 for lift and drag are nearly identical within the line thickness. In comparison to the fine mesh the lift is shifted by SCl « 1LC. The computed lift on the meshes ad3 show the same behaviour. Only the shift to the fine mesh is SCl « 2LC.
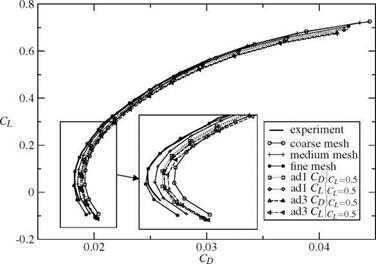
The lift as function of the drag is plotted in figure 4(b). On the refined mesh series the drag reduces by the mesh refinement. The strongest variation of the lift as function of the drag is observable in the region of minimal drag where the curve of the fine mesh is shifted to the left by SCd ~ 10DC in comparison to the drag computed on the coarse mesh. For large angles of attack the reduced drag is nearly completely compensated by the reduced values of the lift so that the curves of the refinement series are close together. For the adapted meshes the shift at the minimal drag is only 8Cd « 3 – 5DC with respect to the results on the coarse mesh. In contrast to the refined meshes the deviation for large angles of attack are getting higher by the number of points.
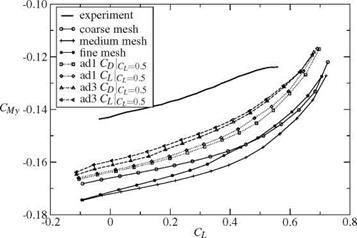
In figure 5 the pitching moment is plotted as function of the lift. The results for the refined mesh series are ambiguous and no trend is observable. The pitching moment on the adapted meshes ad1 and ad3 increases by each refinement.
|
|
|
Fig. 4 (a) Lift Cl as function of the angle of attack a and (b) polar of Cl as function of Cd for the DLR-F6 model. o, + and * denotes the results on the coarse, medium and fine mesh. □ and 0 marks the results on the first adapted mesh at Cl = 0.5 with respect to the lift and drag, respectively. Д and < denotes the results computed on the meshes of the third adaptation step of figure 3. The solid line denotes the experimental results taken from [7]. |
![]()
|
Fig. 5 Pitching moment Сму as function of the lift Cl for the DLR-F6 model. The labels are identical to the labels of figure 4. |
The measurements of [7] are plotted in the figures 4 and 5 as a solid line. Like in the convergence study by trend the lift (angle of attack) and pitching moment of the adapted meshes fits more to the experimental results than the coefficients computed on the refined meshes. The measured lift as function of the drag fits more to the refined meshes.