Estimation of the coefficients of lift, drag and pitching moment from the pressure distribution

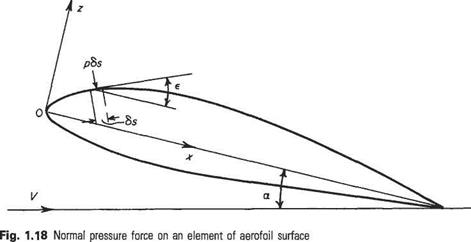
Let Fig. 1.18 represent an aerofoil at an angle of incidences to a fluid flow travelling from left to right at speed V. The axes Ox and Oz are respectively aligned along and perpendicular to the chord line. The chord length is denoted by c.

Taking the aerofoil to be a wing section of constant chord and unit spanwise length, let us consider the forces acting on a small element of the upper aerofoil surface having length 6s. The inward force perpendicular to the surface is given by pu6s. This force may be resolved into components 6X and 6Z in the x and z directions. It can be seen that

6ZU — —pu cos є

and from the geometry

6s cose = 6x
so that

SZU = —pu6x per unit span Similarly, for the lower surface

6Z( = pe6x per unit span

We now add these two contributions and integrate with respect to x between x = 0 and x = c to get

– Г Pudx+ f Jo Jo

But we can always subtract a constant pressure from both pu and pe without altering the value of Z, so we can write

-[ (Pu~Poc)dx+ [ {pe~Poo)d>

JO Jo

where px is the pressure in the free stream (we could equally well use any other constant pressure, e. g. the stagnation pressure in the free stream).

Equation (1.58) can readily be converted into coefficient form. Recalling that the aerofoil section is of unit span, the area S = 1 x c = c, so we obtain

we see that

Cz — f (CPu Cpe)d(x/c)

Jo

or, simply

Cz = <p Cpcosed(.s/c) = <p Cpd(x/c), (1.59b)

Je Jc

where the contour integral is evaluated by following an anti-clockwise direction around the contour C of the aerofoil.

Similar arguments lead to the following relations for X.

6Xu—pu6s sine, SXe = pe6s sine, 6s sin є = 6z,

giving

c*=i Cp sined(s/c) = У Cpd(z/c) = J ACpd^-j, (1.60)

where z^ and zm( are respectively the maximum and minimum values of z, and ACP is the difference between the values of Cp acting on the fore and rear points of an aerofoil for a fixed value of z.

The pitching moment can also be calculated from the pressure distribution. For simplicity, the pitching moment about the leading edge will be calculated. The contribution due to the force 6Z acting on a slice of aerofoil of length 6x is given by

6M = (pu -Pe)x6x – [{pu – Poo) (pt – Poo)]*#;*;

so, remembering that the coefficient of pitching moment is defined as

_ M M. , . „

= mthlst! ase’ as s = c’

the coefficient of pitching moment due to the Z force is given by

CmZ = “i Cp cd(c) = l [Cp" _ Cpf] cd(c) (L61)

Similarly, the much smaller contribution due to the X force may be obtained as

CUX = – jf cr, intjdg = d© (1«)

The integrations given above are usually performed using a computer or graphically.

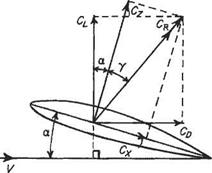
The force coefficients Cx and Cz are parallel and perpendicular to the chord line, whereas the more usual coefficients Cl and Co are defined with reference to the direction of the free-stream air flow. The conversion from one pair of coefficients to the other may be carried out with reference to Fig. 1.19, in which, Cr, the coefficient of the resultant aerodynamic force, acts at an angle 7 to Cz – CR is both the resultant of Cx and Cz, and of CL and CD; therefore from Fig. 1.19 it follows that

Cl = Cr cos(7 + a) = Cr cos 7 cos a — Cr sin 7 sin a

But Cr cos 7 = Cz and Cr sin 7 = Cx, so that

Cl = Cz cos a — Cx sin a. (1.63)

Similarly

Fig. 1.19

The total pitching moment coefficient is

Cm = Cm, + Cm, (1.65)

In Fig. 1.20 are shown the graphs necessary for the evaluation of the aerodynamic coefficients for the mid-section of a three-dimensional wing with an ellipto – Zhukovsky profile.