Example: Parabolic Plate

With d(x) = 4df(1 – c) and d'(x) = 4d(1 – 2c) = 4d cos t, as seen earlier, the Fourier coefficients are easily identified to be

d

A0 = a, A1 = 4 , An = 0, n > 2

c

hence, the vorticity distribution reads

Upon elimination of t in terms of x, the result becomes

(3.64)

Note that this result can be interpreted as the superposition of the flow past a flat plate at incidence (first term proportional to a) plus a parabolic cambered plate at zero incidence (second term proportional to d). It is interesting also to realize that the

Fig. 3.16 Cp distribution for the parabolic plate at zero incidence

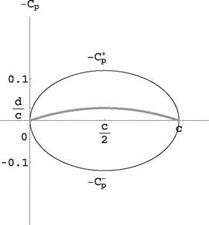
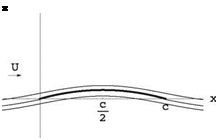Fig. 3.17 Streamlines of the flow past a parabolic plate at zero incidence

parabolic plate at zero incidence satisfies two K – J conditions, one at the trailing edge but also one at the leading edge. Indeed, the angle of adaptation is aadapt = 0. At zero incidence, the parabolic plate has lift and the Cp distributions are half ellipses, as shown in Fig. 3.16.

The flow in this case can be depicted as in Fig.3.17.

Due to the flow symmetry w. r.t the axes x = 2, the lift force will be located at x = xc. p. = §, the center of pressure. When the incidence is positive, the flow will go around the leading edge clockwise and the stagnation point will be located on the lower surface. The opposite is true if the incidence is negative.

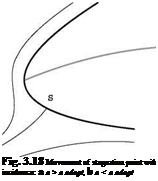
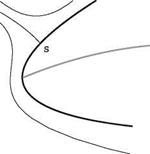
The angle of adaptation has a practical interest for thin cambered plates: at the ideal angle of attack, the viscous effects are minimized because the flow does not have to go around the leading edge with very high velocities and then slow down abruptly, which often provokes separation. However, since it is not possible to control perfectly the incidence of the profile of a wing, thickness is added in the leading edge region that allows the stagnation point to move about the ideal position, without major penalties in viscous effects. See the sketch in Fig.3.18.

(a) (b)