Example Problems

A finite element cyclic symmetry analysis was performed on a LPT turbine rotor (Blade BT). For the first 20 nodal diameter mode the reduced frequency is 0.23 and the mode shapes for the forward traveling wave are

[ —0.260 j [ —0.072 j

{a20c} = < —0.036and {a20s} = < —0.059 [ —0.638 J [ 0.149 J

Since 92.1% of the kinetic energy is in cosine mode, this mode is expected to dominate. The cosine mode has a pitching axis at (£=-0.056, n=0.407). For this location the traditional P-K method plot gives a critical reduced frequency of approximately 0.1. The sine mode has a pitching axis at (£=0.396, n=-0.482) for which the critical reduced frequency is approximately 0.5. Therefore, the traditional method judges the cosine mode to be stable and the sine mode to be unstable.

This case was run using the method described herein with using the blade described in Reference 1 for the baseline work matrices. The results are given in Table 1. As can be seen the total work is dominated by Wcc with a significant contribution from the interaction terms, WC5 and W5C. This interaction terms results in a stabilizing effect for the forward traveling wave and a destabilizing effect for the backward traveling wave. The work associated with the steady pressure has a relatively small effect on the total work. The critical damping ratio, £, is given for both the current method and a that of a full 3D, viscous, CFD method. Both modes are judged to be stable and there is relatively good agreement between methods.

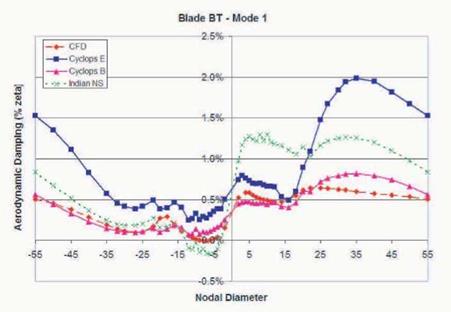
The above analysis was performed for additional nodal diameters and the results are shown in Figure 4.

Table 1. Work and Damping for Blade ВТ, Mode 1, 20 Nodal Diameters Work Component Forward Traveling Wave Backward Traveling Wave wcc -61.6 -40.2 w„ -0.3 0.3 wcs 14.5 10.4 wsc 5.7 4.1 Wps -2.2 2.2 wcyc -72.9 -31.4 c 0.89% 0.39% c (CFD Method) 0.62% 0.27%

The results labeled Cyclops E were obtained using the current method with the baseline work matrices for the blade described in Reference 1 using a 2D inviscid code. Those labeled Cyclops В were obtained using work matrices obtained from a midspan section of blade ВТ, also using a 2D inviscid code. In addition results labeled Indian NS (Navier-Stokes) and Indian Euler are from a similar method developed at the University of Florence [Amone et al., 2003]. The Indian results were based on baseline aerodynamics for blade ВТ. Similar results for the second mode of blade ВТ are shown in Figure 5. For both modes the current method predicts the trends of damping versus nodal diameter reasonably well. With respect to using the current method as a preliminary design screening method, the overall stability is predicted correctly for these two modes (for both baseline work cases).

Blade AT was also analyzed with the new cyclic symmetry method and com­pared with CFD. These comparisons are shown in Figures 6 and 7.

Although not shown, similar comparisons have been made for three modes of two additional blades. For a total of 10 cases the overall stability agrees with the full 3D CFD method in all cases except one, where the current predicts

Figure 4. Aerodynamic Damping for Blade BT Mode 1

Blade BT • Mode 2

instability and the 3D CFD method predicting stability. This type of error is preferred for a preliminary design screening tool.

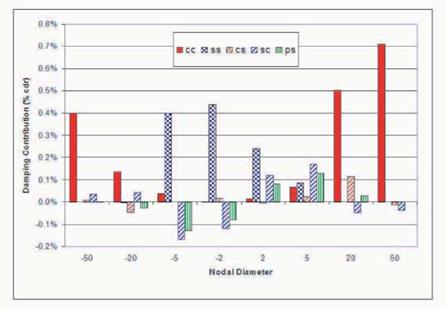
The results for Blade BT were further examined to determine the contri­butions to total damping from the individual work terms. Four representative nodal diameters were selected for study. The 2 nodal diameter mode is nearly a pure sine mode (99.2% of total energy). The 5 nodal diameter mode is predom­inately a sine mode (90.8% of total energy). The 20 nodal diameter mode is predominately a cosine mode (92.1% of total energy). The 50 nodal diameter mode is nearly a pure cosine mode (99.9% of total energy). Figure 5 shows the damping contributions (critical damping ratio) from the Wcc, Wss, Wcs, Wsc, and WPs work terms. That is, the individual work terms are divided by 4n times the total energy. A positive number represents a stabilizing contribution.

The 2 nodal diameter results show that contribution of the interaction terms can be significant for nearly pure real modes. That is, the Wsc contribution is approximately half of the contribution of the Wss. The 5 nodal diameter for­ward traveling wave results show that the interaction term can be the dominant contributor. The effect of the steady pressure terms is anti-symmetric about zero nodal diameters. At 5 nodal diameters the contribution of the steady pres­sure term is larger than that of Wcc and Wss. In this case the contribution of the steady pressure term decreases as the number of nodal diameters is increased.