FUNDAMENTALS OF INVISCID, INCOMPRESSIBLE FLOW
In Chapter 1 it was established that for flows at high Reynolds number the effects of viscosity are effectively confined to thin boundary layers and thin wakes. For this reason our study of low-speed aerodynamics will be limited to flows outside these limited regions where the flow is assumed to be inviscid and incompressible. To develop the mathematical equations that govern these flows and the tools that we will need to solve the equations it is necessary to study rotation in the fluid and to demonstrate its relationship to the effects of viscosity.
It is the goal of this chapter to define the mathematical problem (differential equation and boundary conditions) of low-speed aerodynamics whose solution will occupy us for the remainder of the book.
2.1 ANGULAR VELOCITY, VORTICITY,
AND CIRCULATION
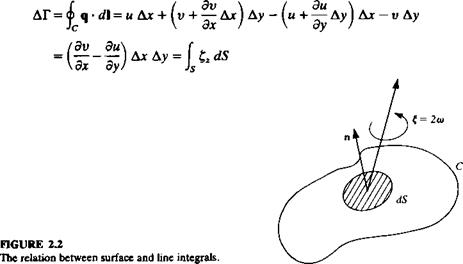
The arbitrary motion of a fluid element consists of translation, rotation, and deformation. To illustrate the rotation of a moving fluid element, consider at t = t0 the control volume shown in Fig. 2.1. Here, for simplicity, an infinitesimal rectangular element is selected that is being translated in the z = 0 plane by a velocity (n, v) of its corner no. 1. The lengths of the sides, parallel
 |
|
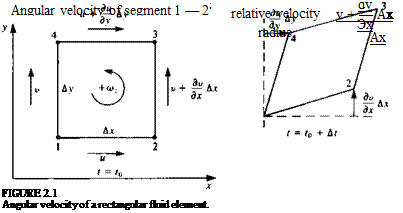
to the x and у directions, are Ajc and Ay, respectively. Because of the velocity variations within the fluid the element may deform and rotate and, for example, the x component of the velocity at the upper corner (no. 4) of the element will be и + (ди/ду)Ау, where higher-order terms in the small quantities Ax and Ay are neglected. At a later time (e. g., t = t0 + At), this will cause the deformation shown at the right-hand side of Fig. 2.1. The angular velocity component (oz (note positive direction in the figure follows the right-hand rule) of the fluid element can be obtained by averaging the instantaneous angular velocities of the segments 1-2 and 1-4 of the element. The instantaneous angular velocity of segment 1-2 is the difference in the linear velocities of the two edges of this segment, divided by the distance (Ax):
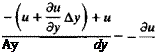 |
and the angular velocity of the 1-4 segment is
The z component of the angular velocity of the fluid element is then the average of these two components
l/dv du
<°z~2di~dy)
The two additional components of the angular velocity can be obtained similarly, and in vector form the angular velocity becomes
![]() ы = tV X q
ы = tV X q
It is convenient to define the vorticity £ as twice the angular velocity.
£ = 2w = VXq (2.2)
In cartesian coordinates the vorticity components are
(dv du
Now consider an open surface S, shown in Fig. 2.2, which has the closed curve C as its boundary. With the use of Stokes’ theorem (see Kellogg,13 p. 73) the vorticity on the surface S can be related to the line integral around C:
I V X q • n dS = j £ • n dS = Ф q • dl
Js ‘s Jc
where n is normal to S. The integral on the right-hand side is called the circulation and is denoted by Г,
Г = <j> q • d (2.3)
This relation can be illustrated again with the simple fluid element of Fig. 2.1. The circulation ДГ is obtained by the evaluation of the closed line integral of the tangential velocity component around the fluid element. Note that the positive direction corresponds to the positive direction of o>.
|
|
For the general three-dimensional case these conclusions can be summarized as Г = <|> q*dl = J Vxq-n</S = jVndS (2.4)
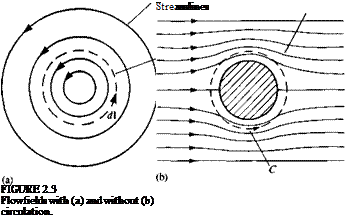
The circulation is therefore somehow tied to the rotation in the fluid (e. g., to the angular velocity of a solid body type rotation). In Fig. 2.3 two examples are shown to illustrate the concept of circulation. The curve C (dashed lines) is taken to be a circle in each case. In Fig. 2.3a the flowfield consists of concentric circular streamlines in the counterclockwise direction. It is clear that along the circular integration path C (Fig. 2.3a) q and d in Eq.
(2.3)
 |
are positive for all d and therefore C has a positive circulation. In Fig.
2.36 the flowfield is the symmetric flow of a uniform stream past a circular cylinder. It is clear from the symmetry that the circulation is zero for this case.
To illustrate the motion of a fluid with rotation consider the control volume shown in Fig. 2.4a, moving along the path l. Let us assume that the viscous forces are very large and the fluid will rotate as a rigid body, while following the path /. In this case V X q Ф 0 and the flow is called rotational. For the fluid motion described in Fig. 2.46, the shear forces in the fluid are negligible, and the fluid will not be rotated by the shear force of the neighboring fluid elements. In this case V X q = 0 and the flow is considered to be irrotational.