Generation of Lift

The very basic theory of aerodynamics lies in the Kutta-Joukowski theorem. This theorem states that for an airfoil with round leading and sharp trailing edge immersed in a uniform stream with an effective angle of attack, there exists a lifting force proportional to the density of air q, free stream velocity U and the circulation Г generated by the bound vortex. Hence, the sectional lifting force I is equal to

I = q U Г (1.1)

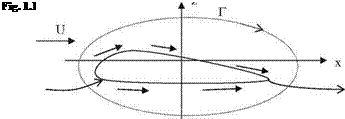
Figure 1.1 depicts the pertinent quantities involved in generation of lift.

The strength of the bound vortex is given by the circulation around the airfoil, Г = H Vds.

If the effective angle of attack is a, and the chord length of the airfoil is c = 2b, with the Joukowski transformation the magnitude of the circulation is found as Г = 2 pa b U. Substituting the value of Г into Eq. 1.1 gives the sectional lift force as

I = 2 qpabU2 (1.2)

Using the definition of sectional lift coefficient for the steady flow we obtain,

I, ,

c = JUb = 2 pa (1:3)

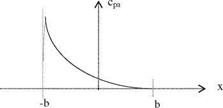
Fig. 1.2 Lifting surface pressure coefficients cpa: theoretical (solid line) and experimental (dotted line)

The very same result can be obtained by integrating the relation between the vortex sheet strength ya and the lifting surface pressure coefficient cpa along the chord as follows.

cpa (x) cpl cpu 2Уа (x) = U

The lifting pressure coefficient for an airfoil with angle of attack reads as

b — x

cpa(x) = 2 a, — b < x < b (1.4)

b + x

Equation 1.4 is singular at the leading edge, x = —b, as depicted in Fig. 1.2. Integrating Eq. 1.4 along the chord and non-dimensionalizing the integral with b gives Eq. 1.3. The singularity appearing in Eq. 1.4 is an integrable singularity which, therefore, gives a finite lift coefficient 1.4. In Fig. 1.2, the comparisons of the theoretical and experimental values of lifting pressure coefficients for a thin airfoil are given. This comparison indicates that around the leading edge the experimental values suddenly drop to a finite value. For this reason, the experi­mental value of the lift coefficient is always slightly lower than the theoretical value predicted with a mathematical model. The derivation of Eq. 1.4 with the aid of a distributed vortex sheet will be given in detail in later chapters.

For steady aerodynamic cases, the center of pressure for symmetric thin airfoils can be found by the ratio the first moment of Eq. 1.1 with the lifting force coef­ficient, Eq. 1.3. The center of pressure and the aerodynamic centers are at the quarter chord of the symmetrical airfoils.

Abbot and Von Deonhoff give the geometrical and aerodynamic properties of so many conventional airfoils even utilized in the present time.