Isentropic Flows

1.7.1 Requirements for isentropy

The specific entropy change ds is defined by the Gibbs relation (1.60), or its equivalent enthalpy form (1.61).

T ds = de + p d(1/p) (1.60)

T ds = dh — (1/p) dp (1.61)

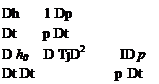Applying these changes d() to a particular fluid element as it moves during some time interval dt, we have d()/dt = D()/Dt. The Gibbs relation (1.61) then becomes a rate equation for the entropy.

Combining {enthalpy eq.(1.38)} — V ■ {momentum eq.(1.36)} produces

which when added to (1.62) gives an alternative expression for the entropy’s material rate of change.

Wherever all three terms on the righthand side are negligible, we have

so that flow regions which are both inviscid and adiabatic must also be isentropic. This is the typical situation outside the viscous layers and without combustion present.