Isentropic relations

Setting ds = 0 in the Gibbs relation (1.61), assuming a calorically-perfect gas with constant cp, and using the ideal gas law (1.13), gives the following three differential equations.

dp dp у dh

p ^ p 7—1 h

These can be integrated to give the three isentropic relations,

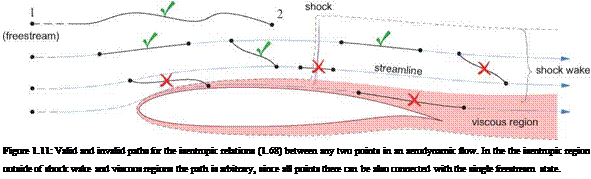where ()i and ()2 are any two states along a particle pathline which is unaffected by viscous stress, heat conduction or addition, or shock losses. For regions whose streamlines are isentropic all the way from far-upstream, points 1 and 2 do not need to lie on the same streamline, as indicated in Figure 1.11.

In steady or unsteady external flows, a common choice for state 1 is the freestream state ()TO, and for state 2 is the state at any point (r, t) in the flow outside of viscous layers or shock wakes, as shown in the upper left of Figure 1.11.

(1.69)

This uniquely relates all the thermodynamic variable fields. These relations, when applicable, can be used as replacements for the energy equation or the streamwise component of the momentum equation.

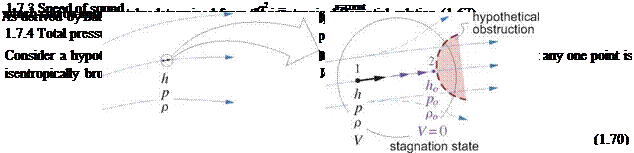Figure 1.12: Isentropic stagnation process from local state 1, to a hypothetical stagnation state 2 denoted by ()o with V =0. This could actually be done by placing a small obstruction in the flow.

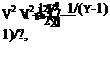Applying the general isentropic relations (1.68) to this process we set p = p and hi = h to be the actual static values at the point, and then set h2 = h0 = h+ V2, which would be the enthalpy at the stagnation state since the total enthalpy cannot change. The corresponding p2 is then defined as the local total pressure,

These Po and pQ же therefore the hypothetical pressure and density at any flow-field point that would result if the enthalpy at that point was isentropically brought to h = ho, or equivalently to the state with V = 0. For this reason po and po are also alternatively called the stagnation pressure and stagnation density.

In aerodynamic flows where the po variation within the flow-field is of particular interest, such as flows with propulsive elements, a convenient non-dimensional form of the total pressure is the total pressure coefficient.

Cpo = P° ~ Po°° (1.74)

In the clean external flow outside viscous layers or propulsive jets we have po=pow and hence Cpo =0.