Lifting Problem
We consider a small element along the x-axis of length d£ with a distribution of vorticity dГ = Г'(£)d£. The contribution of this element to the perturbation stream – function at a point M (x, z) is given in Cartesian coordinates by
Upon integration, this becomes
From this we obtain the perturbation velocity field as
![]() ._дф_ 1 Г ГQz
._дф_ 1 Г ГQz
U x’ z dz 2n J0 (x – £)2 + z2
Note that и is odd and w is even in z, hence < и > = 0 and < w >= 0 across the cut [0, c]. This is consistent with the vortex singularity, see Fig. 3.11.
For the application of the tangency condition on the thin cambered plate at incidence, we let z ^ 0, while 0 < x < c. The condition becomes
Fig. 3.11 Lifting flow z
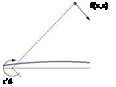 |
|||
induced by a vortex element
MX x,-z)
1 c Гf (£)
w(x, 0) = — —Щd£ = U(d'(x) – a (3.49)
2W0 x – £
The equation above is the fundamental integral equation of thin airfoil theory. In general the airfoil shape d(x) is given as well as the flow conditions U, a. The unknown vorticity Г'(x) is the solution of an integral equation. Once Г’ is found, which satisfies the Kutta-Joukowski condition, Г’ (c) = 0, one can obtain the velocity field everywhere and in particular u(x, 0±) and hence the pressure coefficients on the thin cambered plate, C± (x). Using the result derived earlier with the same singular integrand, the limiting process yields
, , 1 fc Г'(£)г ^ Г ‘(x) f r+
lim u(x, z) = 2 2d£ = = u(x, 0+) (3.50)
z^0+ 2n 0 (x – £)2 + z2 2
It is easy to show by symmetry that u(x, 0-) = – . Across the thin cambered
plate (or cut along the x-axis) the u-component has a jump, < u (x) >= u (x, 0+) – u(x, 0-) = Г'(x). There is also a pressure (or Cp) jump, except at the trailing edge, where the flow leaves the profile “smoothly”. In contrast, the leading edge sustains in general an infinite velocity (Г'(0) = ±to), the only exception being when the leading edge is “adapted”, in which case the flow attaches “smoothly” and satisfies a K – J condition there (Г'(0) = 0), see Fig. 3.12 for typical flow fields at the leading and trailing edges.
The mathematical form of the Kutta-Joukowski condition can be explained by the fact that, if the flow leaves the trailing edge smoothly, the pressures above and below the trailing edge must be equal, hence u+(c) = u -(c) which implies that Г'(c) = 0.











