Low Speed and Incompressible Flows

By considering the governing equations and definitions developed earlier, we can estimate the following typical changes д() of various quantities along a streamline, or more precisely along a particle path.

From ideal gas law (1.13):	Y др ~ (7—1) (h дp + p дН)	(1.75)
From momentum equation (1.36):	др ~ —pVдV	(1.76)
From total enthalpy definition (1.18):	дН ~ дН0 — VдV	(1.77)

Eliminating др between (1.75) and (1.76), eliminating дН using (1.77), and noting that V2/h = (7—1)M2 gives the fractional density change only in terms of fractional V and ho changes.

(1.78)

A low speed flow is defined as one with a negligibly small Mach number everywhere.

M2 ^ 1 (low speed flow) (1.79)

If in addition the flow is adiabatic so that ho ~ constant and hence дН0 = 0, then (1.78) implies

< 1

~ constant along particle path, (1.80)

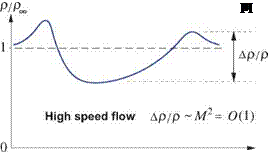
which constitutes an incompressible flow. Figure 1.13 compares typical density variations along a streamline near an airfoil in high speed and low speed flows.

Figure 1.13: In an adiabatic flow, fractional density variations др/р scale as M2 .In the low speed flow case M2 ^ 1 this implies a nearly constant p equal to the freestream value pTO.

For typical aerodynamic flows where the far-upstream density is uniform, the incompressibility result (1.80) becomes the more general statement that the density is constant everywhere in the flow, and equal to the freestream value.

p ~ constant = pTO (incompressible aerodynamic flow) (1.81)

For adiabatic low speed flow where дН0/Н ~ 0, relation (1.77) in addition indicates

д/г h

or h constant

so such flows are also nearly isothermal, and therefore the viscosity p is nearly constant everywhere. In this case the vector identity

V2a + V (V – a)

Va + (Va)T

(1.83)

V-

together with а = V- V = 0, which is the consequence of mass conservation and p = constant, can be used to simplify the viscous momentum term in (1.34) or (1.36) to a Laplacian of the velocity.

p V2V

V ■ T

(1.84)

Overall, the continuity and momentum equations simplify to the incompressible Navier Stokes equations

(1.85)

9V ~dt
+ V V2V
+ V – VV	(1.86)

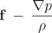
where v = p/p is the kinematic viscosity. The energy and state equations decouple and are no longer needed.