Pitching moment

The pitching moment on a wing may be estimated experimentally by two principal methods: direct measurement on a balance, or by pressure plotting, as described in Section 1.5.6. In either case, the pitching moment coefficient is measured about some definite point on the aerofoil chord, while for some particular purpose it may be desirable to know the pitching moment coefficient about some other point on the chord. To convert from one reference point to the other is a simple application of statics.

Suppose, for example, the lift and drag are known, as also is the pitching moment Ma about a point distance a from the leading edge, and it is desired to find the pitching moment Mx about a different point, distance x behind the leading edge. The situation is then as shown in Fig. 1.10. Figure 1.10a represents the known conditions, and Fig. 1.10b the unknown conditions. These represent two alternative ways of looking at the same physical system, and must therefore give identical effects on the aerofoil.

Obviously, then, L = L and D = D.

Taking moments in each case about the leading edge:

Mle = Ma — La cos a — Da sin a = Mx — Lx cos a — Dx sin a

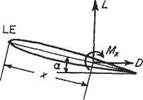Fig. 1.10

then

Mx = Ma — (L cos a + D sin a) (a — x)

Converting to coefficient form by dividing by jpV^Sc gives

CMx = CMa – (CL cos a + CD sin a) (“ – (1.46)

With this equation it is easy to calculate Cmx, for any value of x/c. As a particular case, if the known pitching moment coefficient is that about the leading edge, Смш, then a = 0, and Eqn (1.46) becomes

X

CMx = CMle + – (CL cos a + CD sin a) (1-47)

Aerodynamic centre

If the pitching moment coefficient at each point along the chord is calculated for each of several values of CL, one very special point is found for which Cm is virtually constant, independent of the lift coefficient. This point is the aerodynamic centre. For incidences up to 10 degrees or so it is a fixed point close to, but not in general on, the chord line, between 23% and 25% of the chord behind the leading edge.

For a flat or curved plate in inviscid, incompressible flow the aerodynamic centre is theoretically exactly one quarter of the chord behind the leading edge; but thickness of the section, and viscosity of the fluid, tend to place it a few per cent further forward as indicated above, while compressibility tends to move it backwards. For a thin aerofoil of infinite aspect ratio in supersonic flow the aerodynamic centre is theoretically at 50% chord.

Knowledge of how the pitching moment coefficient about a point distance а behind the leading edge varies with Cl may be used to find the position of the aerodynamic centre behind the leading edge, and also the value of the pitching moment coefficient there, Cmac■ Let the position of the aerodynamic centre be a distance *ac behind the leading edge. Then, with Eqn (1.46) slightly rearranged,

Cm„ = CMде – (Cl cos а + CD sin a) ^

Find the aerodynamic centre and the value of Cm0 ■

It is seen that Cm varies linearly with Cl, the value of dC^/dC/, being

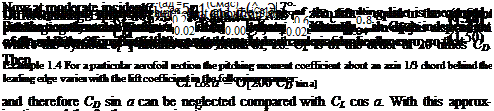0.04 – (-0.02) 0.06

0.80-0.20 -+0.60

Therefore, from Eqn (1.50), with а/с = 1/3

— = i – 0.10 = 0.233 c 3

The aerodynamic centre is therefore at 23.3% chord behind the leading edge. Plotting Су against Cl gives the value of Сма, the value of Cm when Cl = 0, as —0.04.

A particular case is that when the known values of Cm are those about the leading edge, namely CMuL – In this case a = 0 and therefore

Taking this equation with the statement made earlier about the normal position of the aerodynamic centre implies that, for all aerofoils at low Mach numbers:

(1.53)