POTENTIAL FLOW

For a steady, inviscid, incompressible flow, Euler’s equations of fluid motion reduce to two relatively simple relationships that govern the velocity vector.

div V = V • V = 0 (2.43a)

curl V = V x V = 0 (2.43b)

The first equation satisfies conservation of mass; the second one assures that the dynamics of the flow is treated correctly.

In addition to satisfying Equation 2.43 one must assure that any mathe­matical description of the flow field around a given body shape satisfies the boundary condition that there be no velocity normal to the body at all points

on its surface. If n is the unit vector normal to the surface, the following must hold.

V • n = 0 (2.44)

Velocity Potential and Stream Function

To assist in the solution of Equation 2.43, two functions are introduced. The first of these is known as the velocity potential, ф, and is defined such that

(2.45)

Equation 2.45 satisfies identically Equation 2.43b. However, in order to satisfy Equation 2.43a, it follows that ф must be a harmonic function; that is,

V2d> = 0 (2.46)

The operator, V2, known as the Laplacian, is defined as

A flow for which Equation 2.45 is satisfied, and hence ф can be defined, is known as a potential flow. The resulting fluid motion is described as being irrotational. This follows since, in the limit at a point, the curl of the velocity vector, which is zero, is equal to twice the rotational or angular velocity.

The stream function, ф, is related to the velocity components by

дф и = —– ду

дф

v = – ~ дх

ф can only be defined for two-dimensional, or axisymmetric, flow. To obtain a particular component, the partial derivative of ф is taken in the direction normal to the velocity and to the left as one looks in the direction of the velocity.

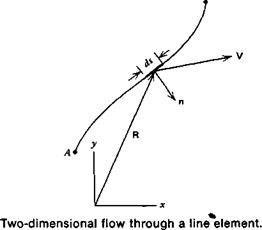
A line element is pictured in Figure 2.11 with flow passing through it. This element is a segment of an arbitrary line connecting two points A and B. The

в

Figure 2.11

iQ = f-dx+¥,ly dx dy

or Thus

dQ = di]/

ф(В) – ф(А) = Tv-ads Ja

(2.48)

That is, the change in the stream function between two points is equal to the flux between the points. It follows that ф is a constant along a streamline. This can be shown by noting that along a streamline

dф = 0

or

ф = constant (along a streamline)

The stream function, as a measure of the flux, satisfies identically Equation 2.43a. For an irrotational flow, however, in order to meet Equation 2.43b it follows that ф must also be harmonic.

V V = 0 (2.49)

In a manner similar to the derivation of Equation 2.48, the change in ф between two points can also be easily obtained. If

ф = ф(х, у)

then

йф = dx + ijL dy dx dy

= и dx + v dy

or, using vector notation,

ф(В) – ф(А) = Г V • dR (2.50)

JA

where R is the radius vector to the curve along which the integration is being performed, as shown in Figure 2.11. dR is then the differential vector along the curve, directed positively, with a magnitude of ds.

As an example in the use of ф and ф, consider the uniform flow pictured in Figure 2.12. For this flow,

и = U = constant v =0

ф will be taken to be zero along the x-axis. This choice is arbitrary, since the values of both ф and ф can be changed by a constant amount without affecting the velocity field obtained from their derivatives. Equation 2.48 will be zero if the integral is performed along a line for which у is a constant.

Figure 2.12 Uniform flow in the x direction.

Thus ф changes only in the у direction. Integrating Equation 2.48 in this direction gives

ФІУ) ~ <K0) = f (iU)idy Jo

от

Ф= Uy

If the uniform flow contains, in addition to U, a constant velocity component V in the у direction, ф becomes

ф = Uy — Vx (2.51)

The minus sign in Equation 2.51 is in accordance with the positive direction of n, as shown in figure 2.11. n is directed to the right as one looks in the direction of point В from point A. In this^case the integration for the second term is in the positive x direction, so n equals – j.

In a more formal manner, ф will be derived for this same flow using Equation 2.50.

V = і 17 + j V

R = ix + j у

Hence

dR = і dx + j dy

so that, taking ф = 0 at x, у = 0,

ф(х, y)= f Udx + Vdy Jo

= Ux + Vy (2.52)